Biết đồ thị hàm số y = x + a x 2 + b x + c có hai điểm cực trị M x 1 ; y 1 ; N x 2 ; y 2 thỏa mãn x 1 y 1 - y 2 = y 1 x 1 - x 2 . Giá trị nhỏ nhất của biểu thức abc+2ab+3c bằng
A. - 49 4
B. - 25 4
C. - 841 36
D. - 7 6
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B và A B = 7 4 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số y = f ( x ) - g ( x ) + m có đúng 5 điểm cực trị?
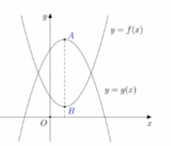
A. 1
B. 3
C. 4
D. 6
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S=-a+b-c+d
![]()
![]()
![]()
![]()
Cho hàm số bậc ba y = ax 3 + bx 2 + cx + d có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Khi đó số điểm cực trị của hàm số y = | ax 2 | x | + bx 2 + c | x | + d | là
A. 5
B. 7
C. 9
D. 11
Cho hai hàm số f ( x ) = x 4 - m - 1 x 2 + 2 và g ( x ) = 2 x 4 - 4 x 2 + 3 m . Giả sử đồ thị hàm số f(x) có ba điểm cực trị là A, B, C và đồ thị hàm số g(x) có ba điểm cực trị là M, N, P. Có bao nhiêu giá trị của tham số m để hai tam giác ABC và MNP đồng dạng với nhau?
A. 1.
B. 0.
C. 2.
D. 3.
Cho hàm số \(y=x^4-2m\left(m+1\right)x^2+m^2\) với m là tham số thực.
a) Tìm m để đồ thị hàm số trên có 3 cực trị tạo thành 3 đỉnh của tâm giác vuông
b) Tìm m để đồ thị hàm số trên có 3 cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Cho hàm số y = f ( x ) có đồ thị như hình vẽ.
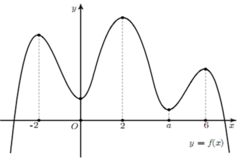
Biết tất cả các điểm cực trị của hàm số y = f ( x ) là – 2, 0, 2, a , 6 với 4 < a < 6. Số điểm cực trị của hàm số y = f ( x 6 − 3 x 2 ) là
A. 8
B. 11
C. 9
D. 7
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng hàm số y=f(x) có m điểm cực trị, hàm số
y
=
f
(
x
)
có n điểm cực trị, hàm số
y
=
f
x
có p điểm cực trị. Giá trị m+n+p là 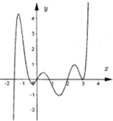
A. 26
B. 30
C. 27
D. 31
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
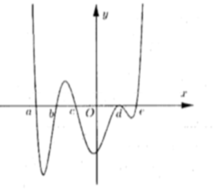
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho hàm số y = f x = a x 3 + b x 2 + c x + d có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S=-a+b-c+d
A. S = 24
B. S = 27
C. S = 31
D. S = 32
cho hàm số y = x 3 − 3 x 2 2 , có đồ thị là (c). gọi m là một điểm thuộc đồ thị (c). viết phương trình tiếp tuyến của ( c) tại m, biết m cùng với hai điểm cực trị của đồ thị tạo thành một tam giác có diện tích bằng 6