Các câu hỏi tương tự
Cho hàm số
f
(
x
)
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3...
Đọc tiếp
Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
,
với m là tham số thực.
Hàm số
g
(
x
)
=
x
2
+
4
x
+
5
x
+
2
có đồ thị C và bảng biến thiên sau:
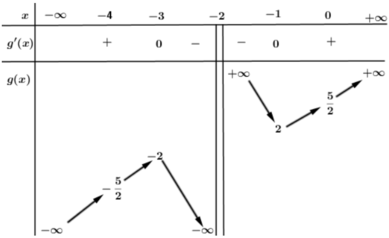
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1
A. m> 2
B. 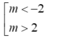
C. m < -5/2
D. m> 5 2
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
y
x
3
-
(
m
+
1
)
x
2
+
(
m
2
-
2
)
x
-
m
2
+
3
có hai điểm cực trị và hai điểm cực trị đó nằm về hai phía khác nhau đối với trục hoành? A. 2 B. 1 C. 3 D....
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 - ( m + 1 ) x 2 + ( m 2 - 2 ) x - m 2 + 3 có hai điểm cực trị và hai điểm cực trị đó nằm về hai phía khác nhau đối với trục hoành?
A. 2
B. 1
C. 3
D. 4
Cho hàm số có đồ thị (C)
y
2
x
+
1
x
-
1
và đường thẳng d: yx+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là A.m1 B.m1 hoặc m5 C.m5 D.m-5
Đọc tiếp
Cho hàm số có đồ thị (C) y = 2 x + 1 x - 1 và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
A.m=1
B.m=1 hoặc m=5
C.m=5
D.m=-5
Cho hàm số y = f(x) = x 4 - 2 ( m - 1 ) x 2 + 1 . Tìm tất cả các giá trị của tham số m để đồ thị hàm số có 3 điểm cực trị lập thành một tam giác vuông.
A. m = -1.
B. m = 0.
C. m = 1.
D. m = 2.
Cho hàm số bậc ba y f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số
y
f
(
x
)
+
m
có 3 điểm cực trị? A. 1 ≤ m ≤ 3 B. m -1 hoặc m 3 C. m ≤ -1 hoặc m ≥ 3 D. m ≤ -3 hoặc m ≥ 1
Đọc tiếp
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x ) + m có 3 điểm cực trị?
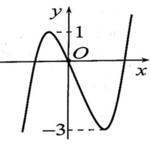
A. 1 ≤ m ≤ 3
B. m = -1 hoặc m = 3
C. m ≤ -1 hoặc m ≥ 3
D. m ≤ -3 hoặc m ≥ 1
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
y
x
3
-
(
m
+
1
)
x
2
+
(
m
2...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 - ( m + 1 ) x 2 + ( m 2 - 2 ) x - m 2 + 3 có hai điểm cực trị và hai điểm cực trị đó nằm về cùng một phía đối với trục hoành?
A. 4
B. 1
C. 3
D. 2