Cho điểm M(1;2;1). Mặt phẳng (P) thay đổi đi qua M lần lượt cắt tia Ox, Oy, Oz tại A, B, C. Giá trị nhỏ nhất của thể tích khối tứ diện OABC là
A. 10
B. 9
C. 18
D. 6
Cho đường thẳng (d) : y = - 2x + 1
a. Điểm nào sau đây thuộc (d):: M(– 1; 3) ; N(1 ; 1) ; K(- 1 /2 ; 0)
b. Tìm toạ độ điểm E thuộc (d)biết Xe = – 2
c.Tìm toạ độ điểm F thuộc(d) biết Yf = 3
d. Cho điểm A( m – 1; 2) thuộc (d) . Tính m ?
b: Thay x=-2 vào (d), ta được:
y=4+1=5
1}Cho 2 tia chung gốc O là Ox và Oy .Trên đường thẳng x lấy điểm O . Trên tia Ox lấy điểm M sao cho OM bằng 2 cm . Trên tia Oy lấy điểm N sao cho ON = 2 cm và OP=a>2cm
a) Chứng tỏ rằng O là trung điểm của MN
b)Tìm giá trị của a sao cho N là trung điểm của OP
2}Cho ddoanj thẳng AB = 2^10 cm . Gọi M-1 là trung điểm của đoạn thẳng AB ; M-2 là trung điểm của doạn thẳng M-1B ; M-3 là trung điểm của đoạn thẳng M-2B ; ... ;M-10 là trung điểm của đoạn thẳng M-9B.Tính độ dài đoạn thẳng M-1;M-9;M-10 .
Trong không gian với hệ tọa độ Oxyz, cho các điểm A 0 ; 4 ; 1 , B − 1 ; 2 ; − 1 và đường thẳng d : x − 1 2 = y − 1 − 1 = z 3 . Trên d lấy điểm M sao cho diện tích tam giác ABM đạt giá trị nhỏ nhất. Gọi M’ là điểm đối xứng với điểm M qua đường thẳng AB. Tổng tọa độ của điểm M’ là:
A. 7 19 .
B. − 14 9
C. 17 9
D. 2
Đáp án B
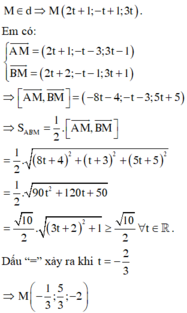
Đường thẳng AB: qua A 0 ; 4 ; 1 vtcp u → = AB → = − 1 ; − 2 ; − 2 ⇒ AB : x = t y = 4 + 2 t z = 1 + 2 t
Gọi H là hình chiếu vuông góc của điểm M trên đường thẳng AB.
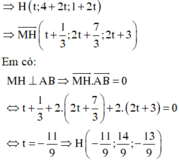
H là trung điểm của MM’ nên M ' − 19 9 ; 13 9 ; − 8 9 .
Vậy tổng tọa độ của điểm M’ là: − 14 9 .
Cho điểm M (m − 1; 2m + 1), điểm M luôn nằm trên đường thẳng cố đinh nào dưới đây ?
A. x – y – 3 = 0
B. 2x – y – 3 = 0
C. 2x – y + 3 = 0
D. Đáp án khác
Cho hàm số y = x 3 - 3 x 2 + 1 có đồ thị (C) và điểm A(1;-1). Xét điểm M bất kì trên (C) có x M = m ( m ≠ 1 ) . Đường thẳng MA cắt (C) tại điểm B (khác M). Tìm tung độ của điểm B.
![]()
![]()
![]()
![]()
1. cho hàm số . tìm điểm cố định
2. cho hàm số
\(y=m^2x^2+2\left(m-1\right)+m^2-1\left(P_m\right)\) . tìm điểm cố định
Bài 1:
\(y=\left(m-1\right)x^2+2mx-3m+1\)
\(=mx^2-x^2+2mx-3m+1\)
\(=m\left(x^2+2x-3\right)-x^2+1\)
Tọa độ điểm cố định mà (Pm) luôn đi qua là:
\(\left\{{}\begin{matrix}x^2+2x-3=0\\y=-x^2+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=-x^2+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\\y=-x^2+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3=0\\y=-x^2+1\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=0\\y=-x^2+1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-3\\y=-\left(-3\right)^2+1=-9+1=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=-1^2+1=0\end{matrix}\right.\end{matrix}\right.\)
Giúp em bài này với ạ:
Câu 16: Trong mặt phẳng toạ độ Oxy, cho hai điểm A(1;-2) ; B(3;2). Tìm điểm M sao cho B là trung điểm của đoạn thẳng AM
A. M(5;6)
B. M(2;0)
C. M(4;0)
D. M(-1;-6)
Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)
Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.
Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.
Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).
Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.
Vậy tọa độ của điểm M là M(2; 0).
Đáp án đúng là: B. M(2; 0).
Bài 1: Cho y=(4m+3)x-m+3 (d)
y=(4m-1)x+3m-1 (d1)
a,Tìm m để (d) cắt (d1) tại 1 điểm trên trục tung
b,Tìm m để (d) cắt (d1) tại 1 điểm trên trục hoành
c,Tìm m để (d) và (d1) cắt nhau tại 1 điểm Bài 2: Cho y=(m-1)x+2m-5 (d2) (m khác 1)
a,Tìm m để phương trình đường thẳng (d2) song song với đường thẳng (d3) y=3x+1
b,Tìm m để phương trình đường thẳng (d2) đi qua M(2;1)
c,Vẽ đồ thị của đường thẳng (d2) với giá trị của m tìm được ở câu b. Tính góc tạo bởi đường thẳng vẽ được với trục hoành
Cho tam giác ABC có D là trung điểm của AC, E là trung điểm của AB. Trên tia CE lấy điểm N sao cho CE = 1/2CN, trên tia BD lấy điểm M sao cho BD = 1/2BM.
C/m: BC=1/2MN
Cho điểm M ( 3 ; 2 ; - 1 ) , điểm đối xứng của M qua mặt phẳng (Oxy) là điểm
A. M'(3;-2;1).
B. M'(3;-2;-1).
C. M'(3;2;1).
D. M'(3;2;0).
Chọn C.
Với M(a, b,c) thì điểm đối xứng của M qua mặt phẳng (Oxy) là M’(a;b;- c).
Do đó, điểm đối xứng với điểm M(3;2;-1) qua mặt phẳng (Oxy) là M’(3;2;1).