Một chất điểm có khối lượng m = 0,1kg dao động điều hòa với phương trình x = 5 c o s 2 t c m . Động năng của vật khi chuyển động qua vị trí có li độ x = 3cm là
A. 0,18J.
B. 0,32mJ.
C. 0,19mJ.
D. 0,32J.
Một chất điểm có khối lượng m = 100g, dao động điều hòa dọc theo trục Ox với phương trình x = 4cos2t cm. Động năng cực đại của chất điểm bằng:
A. 3,2J
B. 0,32J
C. 3200J
D. 0,32mJ
Chọn D
W đ m a x = W t m a x = 1 2 m w 2 A 2 = 0 , 32 . 10 - 3 J = 0 , 32 m J .
Một chất điểm có khối lượng m = 100g, dao động điều hòa dọc theo trục Ox với phương trình x = 4cos(2t) cm. Động năng cực đại của chất điểm bằng
A. 0,32 mJ
B. 3200 J
C. 3,2 J
D. 0,32 J
Đáp án A
Động năng cực đại của chất điểm bằng: w d m a x = 1 2 m ω 2 A 2 = 1 2 . 0 , 1 . 2 2 . 0 , 04 2 = 0 , 32 m J
Một chất điểm có khối lượng m=100g, dao động điều hòa dọc theo trục Ox với phương trình x=4cos(2t) cm. Động năng cực đại của chất điểm bằng
A. 0,32 mJ
B. 3200 J
C. 3,2 J
D. 0,32 J
Đáp án A
Động năng cực đại của chất điểm bằng:
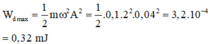
Một chất điểm có khối lượng m = 0,1 kg dao động điều hòa với phương trình x = 5cos2t (cm). Động năng của vật khi chuyển động qua vị trí có li độ x = 3 cm là
A. 0,18 J
B. 0,32 mJ
C. 0,19 mJ
D. 0,32 J
Câu 1: Một chất điểm có khối lượng 200g dao động điều hòa quanh vị trí cân bằng O, phương trình ly độ có dạng x= 2cos(10t) (cm), t tính theo đơn vị giây. Lấy gốc thế năng tại O. Tìm biểu thức động năng của chất điểm
Câu 2: Một chất điểm có khối lượng 100g dao động điều hòa qunah vị trí cân bằng O, phương trình ly độ có dạng x= 6cos(10t) (cm), t tính theo đơn vị giây. Lấy gốc thế năng tại O. Tìm biểu thức thế năng của chất điểm
Bai 1:
\(\omega=\sqrt{\dfrac{k}{m}}\Rightarrow m=\dfrac{k}{\omega^2};v=x'=-\omega A\sin\left(\omega t+\varphi\right)\)
\(W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}\dfrac{k}{\omega^2}.\omega^2A^2.\sin^2\left(\omega t+\varphi\right)=\dfrac{1}{4}kA^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow W_d=\dfrac{1}{4}.\omega^2.m.A^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]=\dfrac{1}{4}.100.0,2.4\left[1-\cos\left(20t\right)\right]=20\left[1-\cos\left(20t\right)\right]\)
Bai 2:
\(W_t=\dfrac{1}{2}kx^2=m\omega^2A^2.\dfrac{\cos\left(2\omega t+\varphi\right)+1}{4}=\dfrac{1}{4}m\omega^2.A^2\left[1+\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow W_t=\dfrac{1}{4}.0,1.100.36.\left[1+\cos\left(2.10t\right)\right]=90.\left[1+\cos20t\right]\)
Bài 1. Một chất điểm dao động điều hòa với phương trình \(x=2cos\left(2\pi t\right)cm.\) Gia tốc của chất điểm tại li độ x = 10 cm là:
A. a = -4 m/s2 B. a = 2 m/s2 C. a = 9,8 m/s2 D. a = 10 m/s2
Bài 2. Một vật dao động điều hòa khi qua VTCB có tốc độ \(8\pi\) \(cm/s\) . Khi vật qua VTB có độ lớn gia tốc là \(8\pi^2\) \(cm/s^2\) . Độ dài quỹ đạo chuyển động của vật là:
A. 16 cm B. 4 cm C. 8 cm D. 32 cm
Bài 1:
Vì xmax = 2cm ⇒ Vật không thể đi qua vị trí có li độ bằng 10 cm.
Em xem lại đề bài bài 1.
Bài 2:
Ta có: \(\left\{{}\begin{matrix}v_{max}=v_{VTCB}=A\omega=8\pi\\a_{max}=a_{VTB}=A\omega^2=8\pi^2\end{matrix}\right.\Rightarrow\omega=\pi\Rightarrow A=8\)
Vậy độ dài quỹ đạo chuyển động là: \(l=2A=2\cdot8=16cm\)
Chọn A.
Em xem lại đề bài nhé em chưa gõ phương trình chuyển động thì không làm được.
Chất điểm có khối lượng m 1 = 50 g a m dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 1 = sin 5 πt + π / 6 . Chất điểm có khối lượng m 2 = 100 g a m dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 2 = 5 sin πt - π / 6 . Tỉ số cơ năng trong quá trình dao động điều hòa của chất điểm m 1 so với chất điểm m 2 bằng
A. 1/2.
B. 2.
C. 1.
D. 1/5.
Một vật nhỏ có khối lượng M = 0,9kg gắn trên một lò xo nhẹ thẳng đứng có độ cứng 25N/m, đầu dưới của lò xo cố định. Một vật nhỏ có khối lượng m = 0,1kg chuyển động theo phương thẳng đứng với tốc độ 0,2√2 m/s đến va chạm mềm với M. Sau va chạm, hai vật dính vào nhau và cùng dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Lấy gia tốc trọng trường g = 10m/s2. Biên độ dao động là:
A. 4,5 cm.
B. 4 cm.
C. 4√2 cm.
D. 4√3 cm.
Chọn B
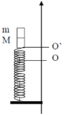
+ Vận tốc của hai vật sau va chạm: (M + m)V = mv
![]()
+ Tọa độ ban đầu của hệ hai vật:
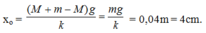
![]()

Chất điểm có khối lượng m 1 = 50 gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 1 = sin ( 5 πt + π / 6 ) (cm). Chất điểm có khối lượng m 2 = 100 gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 2 = 5 sin ( πt - π / 6 ) (cm). Tỉ số cơ năng trong quá trình dao động điều hòa của chất điểm m 1 so với chất điểm m 2 bằng
A. 1/2
B. 2
C. 1
D. 1/5