a: Vì 1+2=3 nên không có tam giác với số đo ba cạnh như vậy

b: Vì 1,2+1<2,4 nên không có tam giác với số đo ba cạnh như vậy

Không có, vì 1,2 + 1 không lớn hơn 2,4.

Gọi độ dài 3 cạnh của tam giác thứ tự là a,b,c (a > 0; b > 0; c > 0).

Vì độ dài 3 cạnh tỉ lệ với 3, 4, 9 nên:

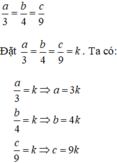
Suy ra: a + b = 3k + 4k = 7k < 9k (hay a + b < c)

Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại)

Vậy không có tam giác nào có 3 cạnh tỉ lệ 3;4;9.

Gọi độ dài 3 cạnh của tam giác thứ tự là a, b, c.

Theo đề bài ta có:

Đặt các tỉ số trên là k. Ta có:

Suy ra: a + b = 3k + 4k = 7k < 9k

Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại).

Vậy không có tam giác nào có 3 cạnh tỉ lệ với 3; 4; 9.

a) Không, vì 2 + 3 = 5.

b) Có, vì 6 + 8 > 10.

Từ định lí cosin trong tam giác ABC, ta suy ra: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)

Mà \({\sin ^2}A + {\cos ^2}A = 1\)

\( \Rightarrow \sin A =  \pm \sqrt {1 - {{\cos }^2}A} \)

Do \({0^o} < \widehat A < {180^o}\) nên \(\sin A > 0\) hay \(\sin A = \sqrt {1 - {{\cos }^2}A} \)

Ta có:

\(\begin{array}{l}\sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}}  = \sqrt {1 - \frac{{{{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} \\ = \sqrt {\frac{{4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}}  = \frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}}\end{array}\)

Thế vào công thức tính diện tích tam giác ABC ta được:

\(S = \frac{1}{2}bc.\frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}} = \frac{1}{4}.\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} \)

Chú ý:

Nếu tiếp tục biến đổi công thức diện tích ta được

\(\begin{array}{l}S = \frac{1}{4}.\sqrt {\left( {2bc + {b^2} + {c^2} - {a^2}} \right)\left( {2bc - {b^2} - {c^2} + {a^2}} \right)} \\ = \frac{1}{4}.\sqrt {\left[ {{{\left( {b + c} \right)}^2} - {a^2}} \right]\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right]} \\ = \frac{1}{4}.\sqrt {\left( {b + c - a} \right)\left( {b + c + a} \right)\left( {a - b + c} \right)\left( {a + b - c} \right)} \end{array}\)

Đến đây, đặt \(p = \frac{{a + b + c}}{2}\), là nửa chu vi tam giác ABC, ta suy ra:

\(\left\{ \begin{array}{l}b + c + a = 2p\\b + c - a = b + c + a - 2a = 2\left( {p - a} \right)\\a - b + c = b + c + a - 2b = 2\left( {p - b} \right)\\a + b - c = b + c + a - 2c = 2\left( {p - c} \right)\end{array} \right.\)

\(\begin{array}{l} \Rightarrow S = \frac{1}{4}\sqrt {2\left( {p - a} \right).2p.2\left( {p - b} \right).2\left( {p - c} \right)} \\ \Leftrightarrow S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \end{array}\)

(công thức Heron)

1m 25cm=125cm

1m 12cm=112cm

1m 11cm=111 cm

Chu vi tam giác là:

125+111+112=348 cm

Đổi 1 m 25 cm = 125 cm

1m12cm=112cm

1m11cm=111cm

Chu vi hình tam giác là:

125+112+111=348(cm)

Đáp số : 348 cm

đổi 1m 25 cm =125 cm

      1m 12 cm = 112 cm

      1m  11 cm = 111 cm

chu vi  hình tam giác là: 

    125 +112 + 111 =348 ( cm )

                            đáp số 348 cm

k mk nha thanks 

Gọi độ dài ba cạnh lần lượtlà a,b,c

Theo đề, ta co: a/2=b/3=c/4

Áp dụng tính chất của DTSBN, ta được;

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{54}{9}=6\)

=>a=12; b=18; c=24

Gọi \(a,b,c\) lần lượt là độ dài 3 cạnh của 1 tam giác 

Theo bài ra ta có : 

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\) và \(a+b+c=54\)

Áp dụng tính chất của dãy tỉ số bằng nhau : 

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{54}{9}=6\)

\(\Rightarrow\left\{{}\begin{matrix}a=6\times2=12\\b=6\times3=18\\c=6\times4=24\end{matrix}\right.\)

Vậy \(12,18,24\) lần lượt là độ dài 3 cạnh của 1 tam giác .