\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7=23-8\sqrt{7}\)

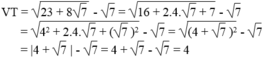
Vế trái bằng vế phải nên đẳng thức được chứng minh.

Xét VT :\(\left(4-\sqrt{7}\right)^2=14-8\sqrt{7}+7=23-8\sqrt{7}\)

=> VT=VP ( đpcm)

b.ta chia B thành 10 nhóm mỗi nhóm có 6 hạng tử  \(B=\left(2+2^2+2^3+2^4+2^5+2^6\right)+....+\left(2^{55}+2^{56}+2^{57}+2^{58}+2^{59}+2^{60}\right)\)

\(B\text{=}2\left(1+2+2^2+2^3+2^4+2^5\right)+...+2^{55}\left(1+2+2^2+2^3+2^4+2^5\right)\)

\(B\text{=}2.63+...+2^{56}.63\)

\(\Rightarrow B⋮63\)

\(\Rightarrow B⋮21\)

Đặt dãy 2 + 2^2 + 2^3 + 2^4 + ... + 2^23 + 2^24 là A 

Theo bài ra ta có : A = ( 2 + 2^2 + 2^3 ) + .... + ( 2^22 + 2^23 + 2^24 )

                           A =  2(1 + 2 + 2^2 ) + ....... + 2^22(1 + 2 + 2^2 )

                           A = 2 . 7 + ......... + 2^22 . 7

                          A = 7( 2 + ............. + 2^22 ) chia hết cho 7

   => A chia hết cho 7 

=> 2 + 2^2 + 2^3 + 2^4 + ..... + 2^23 + 2^24 chia hết cho 7

                               ( điều phải chứng minh )

2+2+2^2+2^3+2^4+...+2^23+2^24

= (2+2^2+2^3)+(2^4+2^5+2^6)+...+(2^22+2^23+2^24)

= 2(1+2+2^2)+ 2^4(1+2+2^2)+....+2^22(1+2+2^2)

= (2+2^4+...+2^22)(1+2+2^2)

= (2+2^4+..+2^22)x7 chia hết cho 7

a) \(\left(\sqrt{5}+2\right)^2=\sqrt{5}^2+4\sqrt{5}+4=5+4\sqrt{5}+4=9+4\sqrt{5}\left(dpcm\right)\)

cậu ơi làm câu 2 lun đi 

a) \(9+4\sqrt{5}=4+4\sqrt{5}+5=2^2+2\cdot2\sqrt{5}+\left(\sqrt{5}\right)^2=\left(\sqrt{5}+2\right)^2\left(ĐPCM\right)\)

a) \(9+4\sqrt{5}=\left(\sqrt{5}\right)^2+2.\sqrt{5}.2+2^2=\left(\sqrt{5}+2\right)^2\left(đpcm\right)\)

b)\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\left(đpcm\right)\)

c)\(\left(4-\sqrt{7}\right)^2=16-8\sqrt{7}+7=23-8\sqrt{7}\left(đpcm\right)\)

d)\(\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{\left(4+\sqrt{7}\right)^2}-\sqrt{7}=4+\sqrt{7}-\sqrt{7}=4\left(đpcm\right)\)

Câu 1: 

$A=(2+2^2)+(2^3+2^4)+(2^5+2^6)+....+(2^{2019}+2^{2020})$

$=2(1+2)+2^3(1+2)+2^5(1+2)+....+2^{2019}(1+2)$

$=(1+2)(2+2^3+2^5+...+2^{2019})=3(2+2^3+2^5+...+2^{2019})\vdots 3$

-----------------

$A=2+(2^2+2^3+2^4)+(2^5+2^6+2^7)+....+(2^{2018}+2^{2019}+2^{2020})$

$=2+2^2(1+2+2^2)+2^5(1+2+2^2)+....+2^{2018}(1+2+2^2)$

$=2+(1+2+2^2)(2^2+2^5+....+2^{2018})$

$=2+7(2^2+2^5+...+2^{2018})$

$\Rightarrow A$ chia $7$ dư $2$.

Câu 2:

$B=(3+3^2)+(3^3+3^4)+....+(3^{2021}+3^{2022})$
$=3(1+3)+3^3(1+3)+...+3^{2021}(1+3)$

$=(1+3)(3+3^3+...+3^{2021})=4(3+3^3+....+3^{2021})\vdots 4$

-------------------

$B=(3+3^2+3^3)+(3^4+3^5+3^6)+...+(3^{2020}+3^{2021}+3^{2022})$

$=3(1+3+3^2)+3^4(1+3+3^2)+....+3^{2020}(1+3+3^2)$

$=(1+3+3^2)(3+3^4+...+3^{2020})=13(3+3^4+...+3^{2020})\vdots 13$ (đpcm)