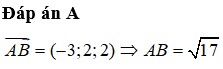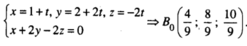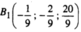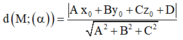Trong không gian Oxyz, cho 2 điểm A(0;3;0), B(0;0;-4) và (P): x+2z=0. Gọi C thuộc trục Ox sao cho mặt phẳng (ABC) vuông góc với mặt phẳng (P). Tọa độ tâm mặt cầu ngoại tiếp tứ diện OABC là
A. ( 1 ; 3 2 ; - 2 )
B. ( - 1 ; - 3 2 ; 2 )
C. ( 1 2 ; 3 2 ; - 1 )
D. ( 1 ; 0 ; - 2 )