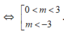Tìm tất cả các giá trị thực của tham số m để điểm M ( 2 m 3 ; m ) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 một tam giác có diện tích nhỏ nhất
A. m = 2
B. m = 0
C. m = 1
D. m = -1
PB
Những câu hỏi liên quan
H24
22 tháng 8 2021 lúc 20:34
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
H24
22 tháng 8 2021 lúc 20:21
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm tất cả các giá trị thực của tham số m để hs y = (m+1).x^4 - mx^2 +3 có 3 điểm cực trị.
Hàm có 3 điểm cực trị khi và chỉ khi:
\(-m\left(m+1\right)< 0\Rightarrow\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
+
m
−
1
4
−
x
2
có 3 điểm cực trị. A.
−
5
;
7
1
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + m − 1 4 − x 2 có 3 điểm cực trị.
A. − 5 ; 7 \ 1
B. − 5 ; 7 \ 1
C. − 1 ; 3 \ 1
D. − 1 ; 3 \ 1
Đáp án A
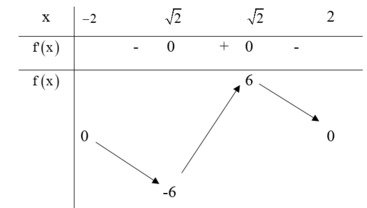
Nhìn vào bảng biến thiên thì điều kiện của m là m − 1 ∈ − 6 ; 6 \ 0 ⇔ m ∈ − 5 ; 7 \ 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
+
m
−
1
4
−
x
2
có 3 điểm cực trị. A.
−
5
;
7
1
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + m − 1 4 − x 2 có 3 điểm cực trị.
A. − 5 ; 7 \ 1
B. − 5 ; 7 \ 1
C. − 1 ; 3 \ 1
D. − 1 ; 3 \ 1
Đáp ánA
Có y ' = 3 x 2 − m − 1 x 4 − x 2 = x 3 x − m − 1 4 − x 2 . y ' = 0 ⇔ x = 0 3 x 4 − x 2 = m − 1 * .
Hàm số có 3 cực trị khi * có 2 nghiệm phân biệt khác 0
* có nghiệm khác 0 ⇔ m − 1 ≠ 0 ⇔ m ≠ 1
Ta lập bảng biến thiên của VT phương trình (*)
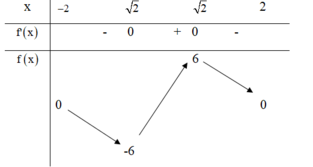
Nhìn vào bảng biến thiên thì điều kiện của m là m − 1 ∈ − 6 ; 6 \ 0 ⇔ m ∈ − 5 ; 7 \ 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số y=x3-(2m+1)x2+m+3 có điểm cực trị?
Tìm tất cả các giá trị thực của tham số m để hàm số
y
(
m
+
1
)
x
4
-
m
x
2
+
3
có ba điểm cực trị. A.
m
∈
(
-
∞
;
-
1
]
∪
[
0
;
+
∞...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = ( m + 1 ) x 4 - m x 2 + 3 có ba điểm cực trị.
A. m ∈ ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ )
B. m ∈ ( - 1 ; 0 )
C. m ∈ ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ )
D. m ∈ ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ )
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
−
3
x
2
+
m
+
1
x
+
2
có hai điểm cực trị. A.
m
2
B.
m
≤
2
C.
m
2
D.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 − 3 x 2 + m + 1 x + 2 có hai điểm cực trị.
A. m < 2
B. m ≤ 2
C. m > 2
D. m < - 4
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
x
+
2
cắt đường thẳng
y
m
-
1
tại 3 điểm phân biệt A.
1
≤
m
≤
5
B.
1
m
5
C.
1
≤
m
5
D.
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 x + 2 cắt đường thẳng y = m - 1 tại 3 điểm phân biệt
A. 1 ≤ m ≤ 5
B. 1 < m < 5
C. 1 ≤ m < 5
D. 1 < m ≤ 5
Tìm tất cả các giá trị thực của tham số m để hàm số
y
m
x
4
+
(
m
2
-
9
)
x
2
+
10
có 3 điểm cực trị B. m -3 C. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x 4 + ( m 2 - 9 ) x 2 + 10 có 3 điểm cực trị
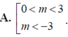
B. m < -3
C. 0 < m ≤ 3
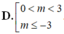
Chọn A
Để hàm số có ba cực trị thì trước hết hàm số phải là hàm số trùng phương tức m ≠ 0
Ta có:
Hàm số có 3 cực trị khi và chỉ khi y ' có 3 nghiệm phân biệt
⇔ m 2 - 9 2 m < 0 ⇔ m ( m 2 - 9 ) < 0
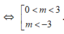
Vậy các giá trị cần tìm của m là 
Đúng 0
Bình luận (0)