Tìm điều kiện xác định của hàm số y = tan x + cot x
PB
Những câu hỏi liên quan
Tìm điều kiện xác định của hàm số
y
tan
x
+
cot
x
A.
x
≠
k
π
,
k
∈
ℤ
B.
x
≠
π
2
+
k
π
,
k
∈
ℤ
C.
x
≠
k
π
2...
Đọc tiếp
Tìm điều kiện xác định của hàm số y = tan x + cot x
A. x ≠ k π , k ∈ ℤ
B. x ≠ π 2 + k π , k ∈ ℤ
C. x ≠ k π 2 , k ∈ ℤ
D. x ∈ ℝ
Tìm tập xác định của các hàm số y = tan x + c o t x
tan x và cos x có nghĩa khi sin x ≠ 0 và cos x ≠ 0
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số sau
y
tan
(
x
-
π
4
)
.
c
o
t
(
x
-
π
3
)
Đọc tiếp
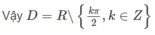
Tìm tập xác định của hàm số sau y = tan ( x - π 4 ) . c o t ( x - π 3 )
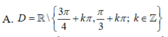
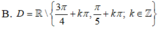
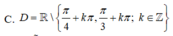
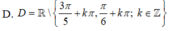
c1 tập xác định của hàm số \(y=\dfrac{sin2x+cosx}{tanx-sinx}\)
c2 tập xác định của hàm số \(y=\sqrt{1+cot^22x}\)
c3 tập xác định của hàm số \(y=cot\left(x-\dfrac{\pi}{4}\right)+tan\left(x-\dfrac{\pi}{4}\right)\)
1.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx}{cosx}-sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
2.
ĐKXĐ: \(sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
3.
ĐKXĐ: \(\left\{{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)\ne0\\cos\left(x-\dfrac{\pi}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{2}\right)\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 2
Bình luận (5)
câu 2 ..... \(\dfrac{cos^22x}{sin^22x}=cot^22x\) nên suy ra sin2x khác 0 đúng hơm
còn câu 3, tui ko hiểu chỗ sin(2x-pi/4).. sao ở đây rớt xuống dợ
Đúng 1
Bình luận (2)
Điều kiện xác định của hàm số
y
c
o
t
x
cos
x
là:
Đọc tiếp
Điều kiện xác định của hàm số y = c o t x cos x là:
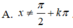
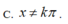
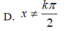
cho hàm số y=f(x)=1/2x-2 tìm điều kiện của x để hàm số y =f(x) xác định
Tìm điều kiện xác định của hàm số
y
x
+
2
-
2
3
A.
x
∈
-
2
;
+
∞
B.
x
≠
-
2
C. Với mọi
x
∈
ℝ...
Đọc tiếp
Tìm điều kiện xác định của hàm số y = x + 2 - 2 3
A. x ∈ - 2 ; + ∞
B. x ≠ - 2
C. Với mọi x ∈ ℝ
D. x ∈ [ 2 ; + ∞ )
Đáp án A
Hàm số y = x α , với không nguyên, có tập xác định là tập các số thực dương.
Do đó hàm số đã cho có tập xác định là 
Đúng 0
Bình luận (0)
Tìm điều kiện xác định của hàm số
y
x
+
2
−
2
3
.
A.
x
∈
−
2
;
+
∞
B.
x
∈
ℝ
C. ...
Đọc tiếp
Tìm điều kiện xác định của hàm số y = x + 2 − 2 3 .
A. x ∈ − 2 ; + ∞
B. x ∈ ℝ
C. x ≠ − 2
D. x ∈ − 2 ; + ∞
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
Đúng 2
Bình luận (0)
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Đúng 2
Bình luận (0)