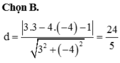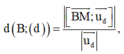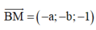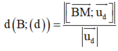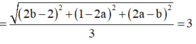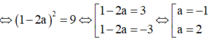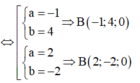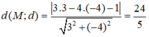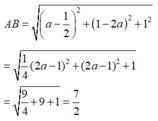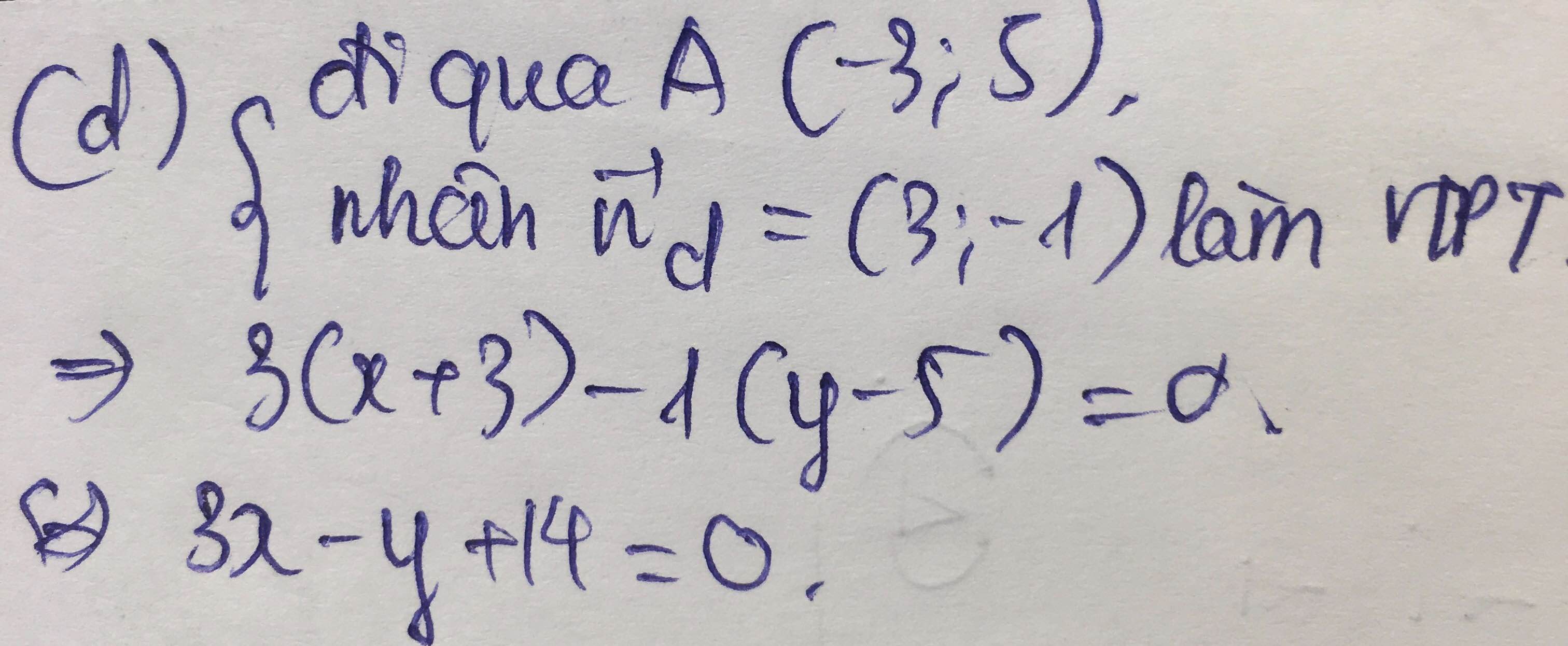1. Trong mặt phẳng toạ độ oxy, cho 2 đường thẳng delta :x+2y+4=0 và d: 2x-y+3=0. Đường tròn tâm I thuộc d cắt Ox tại A và B, cắt trục Oy tại C và D sao cho AB=CD=2. Tính khoảng cách từ điểm I đến đường thăng delta

2. trong mặt phẳng toạ độ oxy, cho tứ giác ABCD với AB:3x-4y+4=0, BC: 5+12y-52=0, CD: 5x-12y-4=0, AD:3x+4y-12=0. tìm điểm I nằm trong tứ giác ABCD sao cho d(I, AB)=d(I,BC)=d(I,CD)=d(I,DA)

Trong mặt phẳng Oxy, khoảng cách từ điểm M (3;-4) đến đường thẳng D: 3x-4y-1=0 

A.  8 5

B.  24 5

C.  12 5

D.  - 24 5

Trong không gian Oxyz, cho mặt phẳng  ( α ) : 2   x + y - 2 z - 2 = 0  đường thẳng d :   x + 1 1 = y + 2 2 = z + 3 2  và điểm  A 1 2 ; 1 ; 1 . Gọi  ∆  là đường thẳng nằm trong mặt phẳng  ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng  ∆  cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng

A.  7 3

B.  7 2  

C.  21 2

D.  3 2

Trong không gian Oxyz, cho mặt phẳng α :   2 x + y - 2 z - 2 = 0 , đường thẳng d :   x + 1 2 = y + 2 2 = z + 3 2  và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng α , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng

A.  7 2

B.  21 2

C. 7 3  

D.  3 2