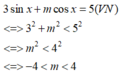Tìm tất cả các giá trị của tham số m để phương trình msinx - mcosx = 2 vô nghiệm
H24
Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số thực m để phương trình
3
sin
x
+
m
cos
x
5
vô nghiệm. A.
m
4
B.
m
−
4
C.
m
≥
4
D.
−
4
m
4
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để phương trình 3 sin x + m cos x = 5 vô nghiệm.
A. m > 4
B. m < − 4
C. m ≥ 4
D. − 4 < m < 4
Tìm tất cả các giá trị thực của tham số m để phương trình
y
5
cos
x
−
m
sin
x
m
+
1
có nghiệm A.
m
≤
12
B.
m
≤
−
13
C.
m
≤
24
D.
m
≥
24
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình y = 5 cos x − m sin x = m + 1 có nghiệm
A. m ≤ 12
B. m ≤ − 13
C. m ≤ 24
D. m ≥ 24
Cho phương trình
sin
x
+
1
sin
2
x
−
m
sin
x
m
cos
2
x
. Tìm tập tất cả các giá trị thực của tham số m để phương trình có nghiệm trên khoảng
0
;...
Đọc tiếp
Cho phương trình sin x + 1 sin 2 x − m sin x = m cos 2 x . Tìm tập tất cả các giá trị thực của tham số m để phương trình có nghiệm trên khoảng 0 ; π 6
A. S = 0 ; 3 2
S. S = 0 ; 1
C. S = 0 ; 1 2
D. S = - 1 ; 3 2
Đáp án A
Phương pháp giải:
Biến đổi công thức lượng giác, đưa phương trình bài cho về dạng phương trình cơ bản, kết hợp với điều kiện nghiệm để tìm giá trị của tham số m
Lời giải:


Đúng 0
Bình luận (0)
Câu 3. Tìm tất cả các giá trị của tham số m để phương trình mcosx+m-1=0 có nghiệm thuộc đoạn 0 ; pi/2. Giúp em với, em cảm ơn.
Tìm tất cả giá trị thực của tham số m để phương trình (cosx+1)(cos2x-mcosx)
m
sin
2
x
có đúng hai nghiệm
x
∈
0
;
2
π
3
. A.
0
≤
m
1
B.
-
1
m
≤
-...
Đọc tiếp
Tìm tất cả giá trị thực của tham số m để phương trình (cosx+1)(cos2x-mcosx)= m sin 2 x có đúng hai nghiệm x ∈ 0 ; 2 π 3 .
A. 0 ≤ m < 1
B. - 1 < m ≤ - 3 2
C. - 1 < m ≤ - 1 2
D. - 3 2 ≤ m < 1
1. Tìm tất cả các giá trị thực của tham số m để hàm số y= mx - sin3x đồng biến trên khoảng ( trừ vô cùng ; cộng vô cùng) 2. Tìm tất cả các giá trị thực của tham số m để hàm số y = x + mcosx đồng biến trên khoảng( trừ vô cùng ; cộng vô cùng)
1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
Đúng 1
Bình luận (0)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)
Đúng 1
Bình luận (0)
Cho phương trình (m+1)sinx + mcosx 2m-1 với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình có nghiệm. Tính tổng tất cả các phần tử của S.
Đọc tiếp
Cho phương trình (m+1)sinx + mcosx = 2m-1 với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình có nghiệm. Tính tổng tất cả các phần tử của S.
![]()
![]()
![]()
![]()
1. Các nghiệm của phương trình \(\sqrt{3}sin2x-cos2x-2=0\) là?
2. Hàm số \(y=2cos3x+3sin3x-2\) có tất cả bao nhiêu giá trị nguyên dương?
3. Tìm tham số m để phương trình \(msinx-cosx=\sqrt{5}\) có nghiệm
Giúp mk với ạ!
1, Phương trình tương đương
\(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
⇔ \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
⇔ \(2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k.2\pi\)
⇔ x = \(\dfrac{\pi}{3}+k.\pi\)
2, \(2cos3x+3sin3x-2\)
= \(\sqrt{13}\)\((\dfrac{2}{\sqrt{13}}cos3x+\dfrac{3}{\sqrt{13}}sin3x)\) - 2
Do \(\left(\dfrac{2}{\sqrt{13}}\right)^2+\left(\dfrac{3}{\sqrt{13}}\right)^2=1\) nên tồn tại 1 góc a sao cho \(\left\{{}\begin{matrix}sina=\dfrac{2}{\sqrt{13}}\\cosa=\dfrac{2}{\sqrt{13}}\end{matrix}\right.\)
BT = \(\sqrt{13}sin\left(x+a\right)-2\)
Do - 1 ≤ sin (x + a) ≤ 1 với mọi x và a
⇒ \(-\sqrt{13}-2\le BT\le\sqrt{13}-2\)
⇒ \(-5,6< BT< 1,6\)
Vậy BT nhận 5 giá trị nguyên trong tập hợp S = {-5 ; -4 ; -3 ; -2 ; -1}
3. \(msinx-cosx=\sqrt{5}\)
⇔ \(\dfrac{m}{\sqrt{m^2+1}}.sinx-\dfrac{1}{\sqrt{m^2+1}}.cosx=\dfrac{\sqrt{5}}{\sqrt{m^2+1}}\)
⇔ sin(x - a) = \(\sqrt{\dfrac{5}{m^2+1}}\) với \(\left\{{}\begin{matrix}sina=\dfrac{1}{\sqrt{m^2+1}}\\cosa=\dfrac{m}{\sqrt{m^2+1}}\end{matrix}\right.\)
Điều kiện có nghiệm : \(\left|\sqrt{\dfrac{5}{m^2+1}}\right|\le1\)
⇔ m2 + 1 ≥ 5
⇔ m2 - 4 ≥ 0
⇔ \(\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để phương trình 3sinx - 5cosx = m vô nghiệm.