Cho hình vẽ bên. Biết A O C ^ + B O D ^ = 140°.
Hãy tính số đo các góc A O C ^ ; C O B ^ ; B O D ^ và D O A ^
Cho hình vẽ bên:
Hãy tính diện tích phần tô màu?
Cho hình vẽ sau, điền vào chỗ trống cho đúng:

a) Các điểm nằm trên đường tròn (O) là: ...
b) Các điểm nằm bên ngoài đường tròn (O) là: ...
c) Các điểm nằm bên trong đường tròn (O) là: ...
d) Các dây của đường tròn (O) là: ...
e) Đường kính của đường tròn (O) là
a) A, B, C, D
b) G, H
c) I, F
d) AB, CD
e) BE
Cho hình vẽ sau, điền vào chỗ trống cho đúng:

a) Các điểm nằm trên đường tròn (O) là: ...
b)Các điểm, nằm bên ngoài, đường tròn (O) là: ...
c) Các điểm nằm bên trong đường tròn (O) là: ...
d) Các dây của đương tròn (O) là: ...
e) Đường kính của đường tròn (O) là:
a) M, BN, C, D
b) B, K
c) A, I, G
d) CN
e) MN
Cho hình vẽ sau, điền vào chỗ trống cho đúng:
a) Các điểm nằm trên đường tròn (O) là: ...
b) Các điểm nằm bên ngoài đường tròn (O) là: ...
c) Các điểm nằm bên trong đường tròn (O) là: ...
d) Các dây của đường tròn (O) là: ...
e) Đường kính của đường tròn (O) là: ...

a) A, B, C, D
b) G, H
c) I, F
d) AB, CD
e) BE.
Cho hình vẽ sau, điền vào chỗ trống cho đúng:
a) Các điểm nằm trên đường tròn (O) là: ...
b)Các điểm, nằm bên ngoài, đường tròn (O) là: ...
c) Các điểm nằm bên trong đường tròn (O) là: ...
d) Các dây của đương tròn (O) là: ...
e) Đường kính của đường tròn (O) là: ...

a) M, BN, C, D
b) B, K
c) A, I, G
d) CN
e) MN.
Cho hình vẽ sau, điền vào chỗ trống cho đúng:
a) Các điểm nằm trên đường tròn (O) là: ...
b) Các điểm nằm bên ngoài đường tròn (O) là: ...
c) Các điểm nằm bên trong đường tròn (O) là: ...
d) Các dây của đường tròn (O) là: ...
e) Đường kính của đường tròn (O) là: ...

a) A,M, B.
b) N, E.
c) Q, P.
d) MA, MB.
e) AB
Cho hình vẽ bên: a) Chứng minh: tam giác OCB = tam gíác ODE
b) Chứng minh: góc B = góc E
c) Chứng minh: BC // DE ![]()
a: Xét ΔOCB và ΔODE có
OC=OD
CB=DE
OB=OE
Do đó: ΔOCB=ΔODE
Bài 1. Cho hình vẽ bên biết AOC+BOD=140.TÍnh AOC,COB,BOD,DOA
Bài 3. Đường thẳng xx' cắt dường thẳng yy' từ O. Vẽ tia phân giác Ot của góc xOy
a) Gọi Ot' là tia đôi của tia Ot. So sánh xOt' và t'Oy.
b) Vẽ tia phân giác Om của góc xOy'. Tính góc mOt
Bài 1:
Vì ∠AOC = ∠BOD (đối đỉnh)
Vì ∠AOC + ∠BOD = 140o (gt)
⇒ ∠AOC = ∠BOD = 140o/2 = 70o
Ta có: ∠AOC + ∠AOD = ∠COD (2 góc kề bù)
Thay số: 70o + ∠AOD = 180o
∠AOD = 180o - 70o
∠AOD = 110o
Vì ∠AOD = ∠BOC (đối đỉnh)
⇒ ∠BOC = 110o
Vậy ∠AOC = 70o
∠BOD = 70o
∠AOD = 110o
∠BOC = 110o
1.
Ta có: ∠AOC+ ∠BOD= 140o
Mà 2 góc này là 2 góc đối đỉnh
⇒ ∠AOC= ∠BOD= 70o
Ta lại có:
∠AOD+ ∠DOB= 180o ( Hai góc kề bù )
⇒ ∠AOD= 110o
Do BOC và AOD là 2 góc đối đỉnh
⇒ ∠BOC= 110o\(^{ }\)
Vậy...
Cho hình vẽ sau, điền vào chỗ trống cho đúng:

Các điểm nằm trên đường tròn (O) là: ...
b) Các điểm nằm bên ngoài đường tròn (O) là: ...
c) Các điểm nằm bên trong đường tròn (O) là: ...
d) Các dây của đường tròn (O) là: ...
e) Đường kính của đường tròn (O) là: ...
a) A,M, B.
b) N, E.
c) Q, P.
d) MA, MB.
e) AB
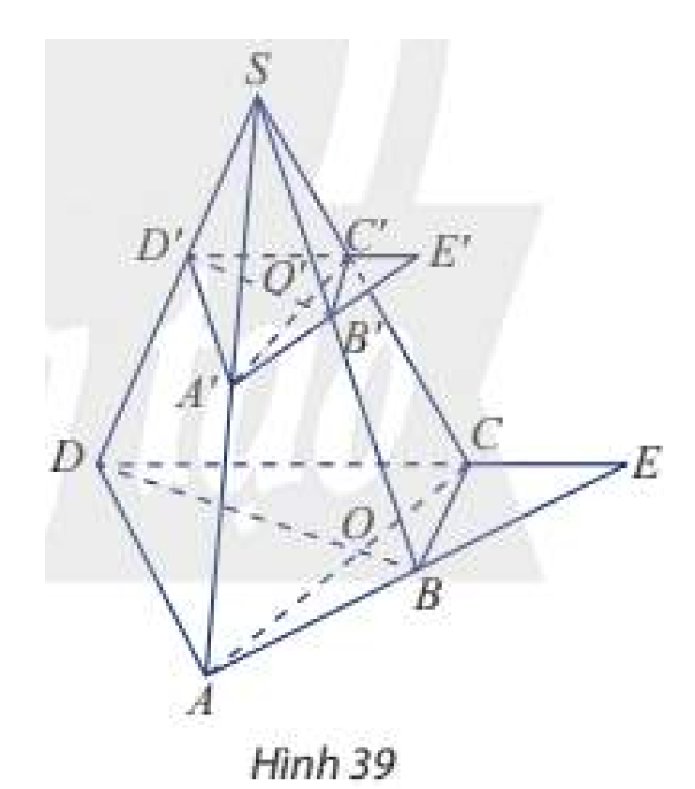
Cho hình chóp \(S.ABCD\). Trên các cạnh bên của hình chóp lấy lần lượt các điểm \(A',B',C',D'\). Cho biết \(AC\) cắt \(B{\rm{D}}\) tại \(O\), \(A'C'\) cắt \(B'{\rm{D'}}\) tại \(O'\), \(AB\) cắt \(DC\) tại \(E\) và \(A'B'\) cắt \(D'C'\) tại \(E'\) (Hình 39). Chứng minh rằng:
a) \(S,O',O\) thẳng hàng;
b) \(S,E',E\) thẳng hàng.
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in BD \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}O' \in A'C' \subset \left( {SAC} \right)\\O' \in B'D' \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O' \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
Do đó, \(S,O,O'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Vậy \(S,O',O\) thẳng hàng.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in AB \subset \left( {SAB} \right)\\E \in CD \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\\left. \begin{array}{l}E' \in A'B' \subset \left( {SAB} \right)\\E' \in C'D' \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E' \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\)
Do đó, \(S,E,E'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\).
Vậy \(S,E,E'\) thẳng hàng.