Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; -4); P(-1; 6) lần lượt là trung điểm của các cạnh BC; CA; AB. Tìm tọa độ đỉnh A?
A. A(1; 5)
B. A(-3; -1)
C. A(-2; -7)
D. A(1; -10)
Trong hệ tọa độ Oxy cho tam giác ABC có A(3 ; 5) ; B( 1 ;2) và C( 5 ;2). Tìm tọa độ trọng tâm G của tam giác ABC ?
A. G( -9 ; -9)
B. G 9 2 ; 9 2
C. G( 3 ;3)
D. G(9 ; 9)
Trong hệ tọa độ Oxy cho tam giác ABC có A(3 ; 5) ; B( 1 ;2) và C( 5 ;2). Tìm tọa độ trọng tâm G của tam giác ABC ?
A. G( -9 ; -9)
B. 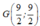
C. G( 3 ;3)
D.G(9 ; 9)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Trong hệ trục tọa độ Oxy, cho tam giác ABC có A(2;–2), B(1;–1), C(5;2). Độ dài đường cao AH của tam giác ABC là
A. 3 5
B. 7 5
C. 9 5
D. 1 5
Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2) 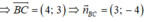
(BC): 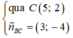
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
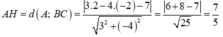
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G 2 3 ; 0 , biết M(1;1) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A.(2;0)
B.(-2;0)
C.(0;-2)
D.(0;2)
Trong hệ tọa độ Oxy ; cho tam giác ABC có A(-2 ; 2) : B(3 ; 5) và trọng tâm là gốc tọa độ O(0 ; 0). Tìm tọa độ đỉnh C?
A. C(-1 ; - 7)
B. C( 2 ; -2)
C. C(-3 ; -3)
D. (1 ; 7)
Trong hệ tọa độ Oxy ; cho tam giác ABC có A(-2 ; 2) : B(3 ; 5) và trọng tâm là gốc tọa độ O(0 ; 0). Tìm tọa độ đỉnh C?
A. C(-1 ; - 7)
B. C( 2 ; -2)
C. C(-3 ; -3)
D. (1 ; 7)
Chọn A.
Gọi tọa độ điểm C( x ; y)
Vì O là trọng tâm tam giác ABC nên 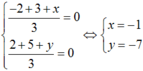
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có các đỉnh A(-1;0); B(4;0);C(0;m).
Tìm tọa độ trọng tâm G của tam giác ABC theo m. Tìm m để tam giác GAB vuông tại G
Gọi \(\left(x_G;y_G\right)\) là tọa độ của G. Theo công thức tính trọng tâm tam giác, ta có :
\(\begin{cases}x_G=\frac{-1+4+0}{3}=1\\y_G=\frac{0+0+m}{3}=\frac{m}{3}\end{cases}\)
Vậy \(G\left(1;\frac{m}{3}\right)\)
\(\widehat{AGB}=90^0\Leftrightarrow\overrightarrow{BG}\perp AG\Leftrightarrow\overrightarrow{BG}.\overrightarrow{AG}=0\) (1)
\(\overrightarrow{BG}=\left(1-4;\frac{m}{3}-0\right)=\left(-3;\frac{m}{3}\right)\)
\(\overrightarrow{AG}=\left(1+1;\frac{m}{3}-0\right)=\left(2;\frac{m}{3}\right)\)
\(\overrightarrow{BG}.\overrightarrow{AG}=\frac{m^2}{9}-6\) (2)
Thay (2) vào (1) ta có : \(\widehat{AGB}=90^0\Leftrightarrow m^2=54\Leftrightarrow m=\pm3\sqrt{6}\)
Vậy có 2 giá trị cần tìm của m
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G ( 2 3 ; 0 ) , biết M ( 1 ; 1 ) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A. (2;0)
B. (-2;0)
C. (0;-2)
D. (0;2)