Hypebol có hai tiêu điểm là F1(-2;0) và F2 (2;0) và một đỉnh A(1;0) có phương trình là chính tắc là
A. 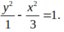
B. 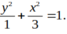
C. 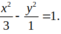
D. 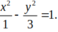
cho đường hypebol có phương trình 9x2 - 3y2 = 1 khoảng cách giữa hai tiêu điểm của hypebol là
9x^2-3y^2=1
=>\(\dfrac{x^2}{\dfrac{1}{9}}-\dfrac{y^2}{\dfrac{1}{3}}=1\)
=>a=1/3; b=1/căn 3
\(c^2=b^2-a^2=\dfrac{1}{3}-\dfrac{1}{9}=\dfrac{2}{9}\)
=>\(c=\dfrac{\sqrt{2}}{3}\)
=>\(2c=\dfrac{2\sqrt{2}}{3}\)
Hypebol x 2 16 - y 2 9 = 1 có hai tiêu điểm là:
A. F1(-5;0), F2(5;0)
B. F1(-2;0), F2(2;0)
C. F1(-3;0), F2(3;0)
D. F1(-4;0), F2(4;0)
Đáp án: A
Hypebol x 2 16 - y 2 9 = 1 có a 2 = 16, b 2 = 9
⇒ c 2 = a 2 + b 2 = 16 + 9 = 25
Vậy hypebol x 2 16 - y 2 9 = 1 có tiêu điểm là F1(-5;0), F2(5;0)
Hypebol x 2 16 - y 2 9 = 1 có hai tiêu điểm là :
A. F1( -5;0) và F2(5;0)
B. F1( -2;0) và F2(2;0)
C. F1( - 3;0) và F2(3;0)
D. F1( -4;0) và F2(4;0)
Chọn A.
Ta có: a 2 = 16 b 2 = 9 c 2 = a 2 + b 2 ⇒ a = 5 b = 3 c = 5
Các tiêu điểm là F1( -5;0) và F2(5;0).
Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H7.25). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.
Ta có: \(AM = BM = CN = DN,AN = BN = CM = DM\). Từ đó suy ra
\(\left| {AM - AN} \right| = \left| {BM - BN} \right| = \left| {CM - CN} \right| = \left| {DM - DN} \right| \).
Và \(\left| {AM - AN} \right| <MN\) (bất đẳng thức trong tam giác)
Vậy bốn điểm \(A,B,C,D\) cùng thuộc một đường hyperbol với M,N là hai tiêu điểm.
Vẽ hình trong mỗi trường hợp sau:
a) Vẽ hypebol biết hai tiêu điểm \({F_1}( - 5;0),{F_2}(5;0)\) và điểm \((3;0)\) thuộc hypebol;
b) Vẽ parabol biết phương trình chính tắc: \({y^2} = 5x\);
c) Vẽ elip tại các giá trị \(a = 3,b = 1\) và \(a = 6,b = 3,5.\)
a) Nhập lệnh: Hypebon((-5,0),(5,0),(3,0)) vào ô nhập lệnh rồi bấm enter.
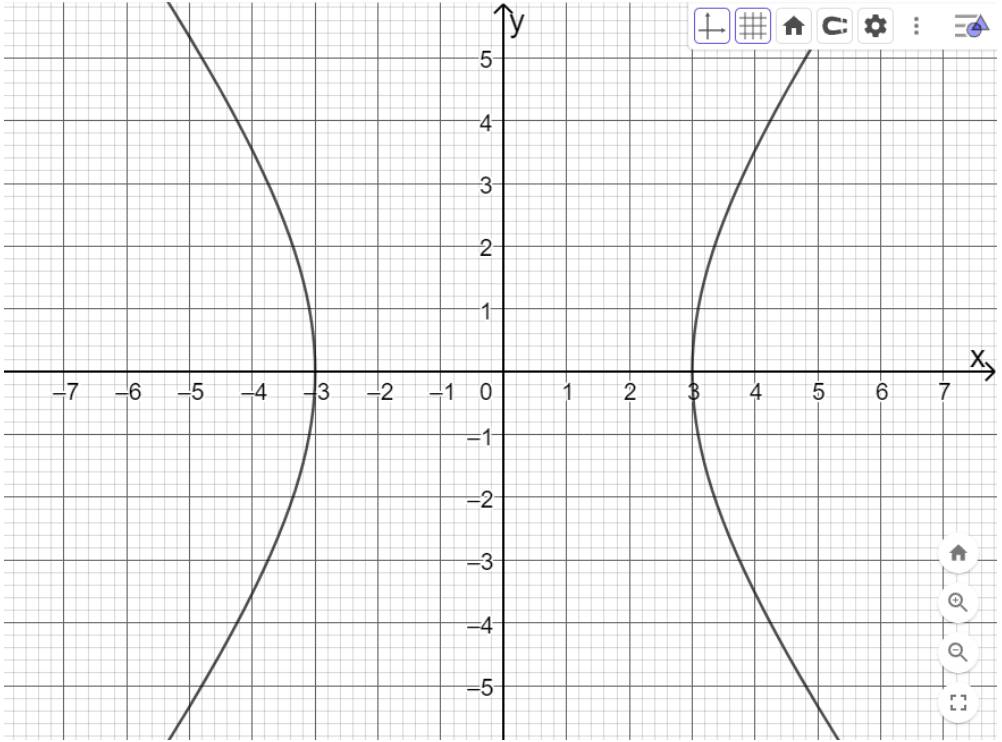
b) Nhập lệnh: y^2=5*x vào ô nhập lệnh rồi bấm enter
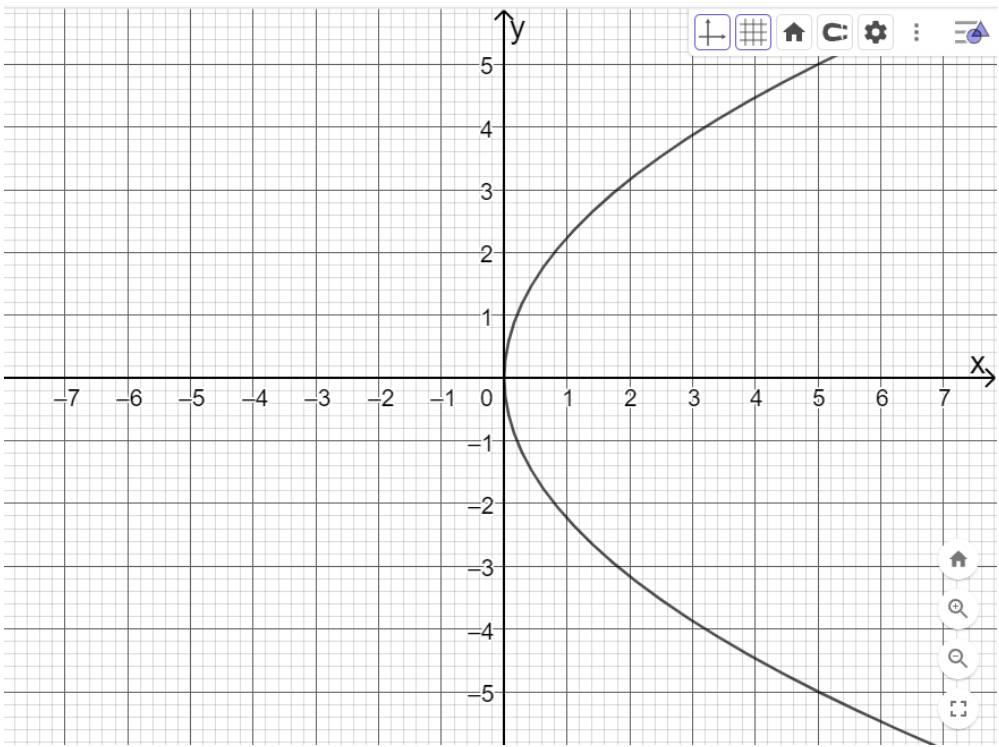
c)
Bước 1: Tạo thanh trượt a: Nháy vào biểu tượng thanh trượt, sau đó nháy cuột lên vùng làm việc, khi đó trên vùng làm việc xuất hiện bảng cho phép thiết lập thông tinh cho thanh trượt: Tên thanh trượt (a), giá trị dạng số/ số nguyên, giá trị cực tiểu (1), giá trị cực đại (10).
Bước 2: Tạo thanh trượt b: Làm tương tự với thiết lập thông tin chẳng hạn như:
Tên thanh trượt (b), giá trị dạng số, giá trị cực tiểu (0), giá trị cực đại (5), số gia (0,5).
Bước 3: Nhập phương trình chính tắc của elip vào ô Nhập lệnh:
x^2 / a^2 + y^2 / b^2 =1 và bấm enter.
Di chuyển trên thanh trượt vào giá trị a=3, b=1 ta được như hình dưới
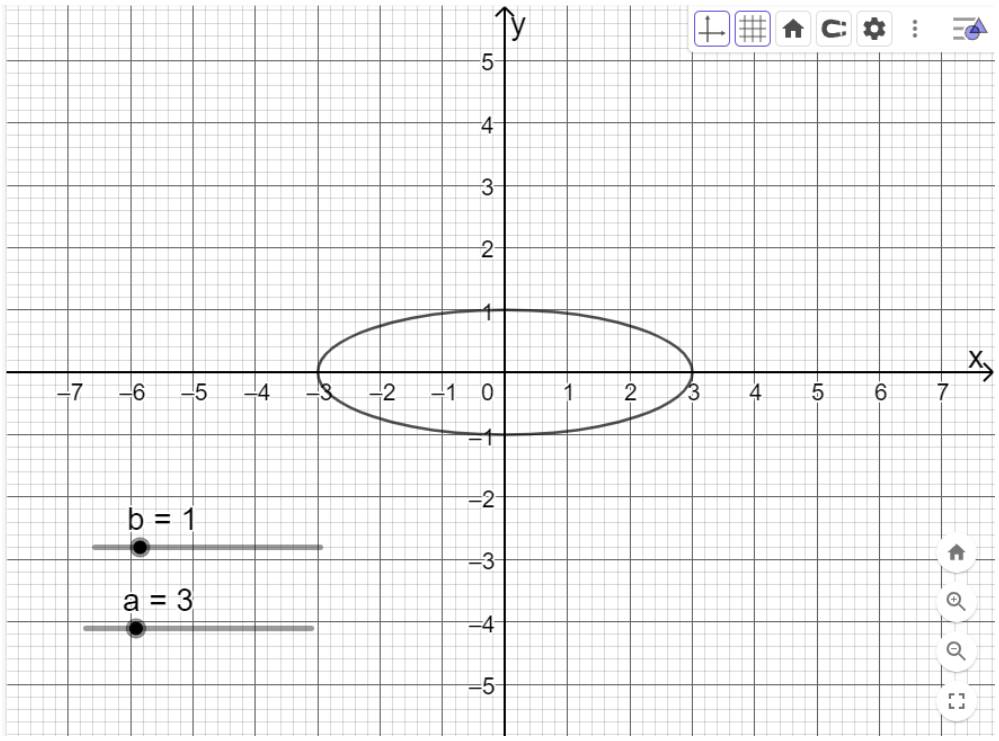
Di chuyển trên thanh trượt vào giá trị a=6, b=3,5 ta được như hình dưới
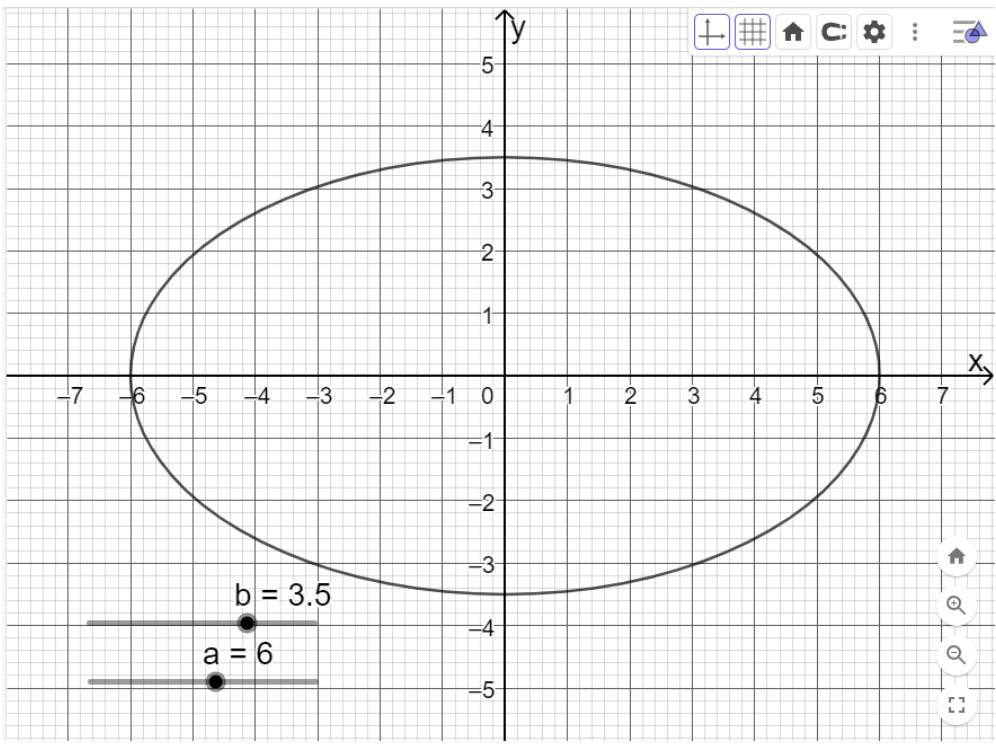
Viết phương trình chính tắc của:
a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16
b) Hypebol có tiêu cự \(2c = 20\) và độ dài trục thực \(2a = 12\)
c) Parabol có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\)
a) Ta có \(2a = 20 \Rightarrow a = 10,2b = 16 \Rightarrow b = 8\).
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
b) Ta có \(2a = 12 \Rightarrow a = 6,2c = 20 \Rightarrow c = 10\), suy ra \(b = \sqrt {{c^2} - {a^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)
Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{64}} = 1\)
c) Ta có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\).
Do đó, \(\frac{p}{2} = \frac{1}{2}\) suy ra \(p = 1\).
Vậy phương trình chính tắc của parabol là \({y^2} = 2x\).
Hypebol có nửa trục thực là 4, tiêu cự bằng 10 có phương trình chính tắc là:
A. 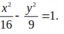
B. 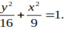
C. 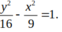
D. 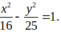
Chọn B
Ta có a = 4 2 c = 10 b 2 = c 2 - a 2 ⇒ a = 4 c = 5 b = 3
Phương trình chính tắc của Hyperbol là
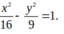
Lập phương trình chính tắc của hypebol biết 1 tiêu điểm là F(-1; 0) và 1 đường tiệm cận là 3x + y = 0
Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào ( elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.
a) \({y^2} = 18x\)
b) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\)
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)