Cho các vectơ a → ; b → . Khẳng định nào sau đây là đúng?
A. a → − b → a → + b → = a → 2 − b → 2
B. a → − b → 2 = a → 2 + b → 2
C. a → + b → a → + b → = a → 2 − b → 2
D. a → + b → a → + b → = a → 2 + b → 2
Cho hình thôi ABCD tâm I. Hãy cho biết số khẳng định đúng trong các khẳng định sau?
a. vectơ AB = vectơ BC
b. vectơ AB = vectơ DC
c. vectơ IA = vectơ IO
d. vectơ IB = vectơ IA
e. |vectơ AB| = |vectơ BC|
f. 2|vectơ IA| = |vectơ BD|
A. 3
B. 4
C. 5
D. 6
Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ khác vectơ O→ và cùng phương với vectơ OA→.
b) Tìm các vectơ bằng vectơ AB→.
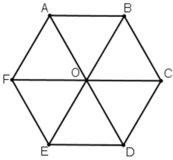
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
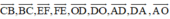
b) Các vectơ bằng vectơ AB→ là:
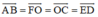
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)
Cho các vectơ a → ( 1 ; 3 ) ; b → ( 2 ; 5 ) ; c → ( 7 ; 19 ) . Phân tích vectơ c → theo các vectơ a → ; b → là:
A. c → = 3 a → + 2 b →
B. c → = 3 a → - 2 b →
C. c → = 2 a → + 3 b →
D. c → = 2 a → - 3 b →
Cho hình bình hành ABCD có O = AC n BD a,Tìm các vectơ khác vectơ O + Cùng phương với vectơ OA + Cùng chiều với vectơ BD b, Tìm các vectơ + bằng với AB + bằng với CO
Trong mặt phẳng tọa độ,cho vectơ u=1/2 vectơ i -5 vectơ j và vectơ v=K vectơ i -4 vectơ j a)tìm các giá trị của K để | vectơ u|=| vectơ v| Giúp tui với mng
Với hai vectơ \(\overrightarrow a ,\overrightarrow b \) cho trước, lấy một điểm A vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ khác A và cũng vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\;\overrightarrow {B'C'} = \overrightarrow b \). Hỏi hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) có mối quan hệ gì?
\(\overrightarrow {AB} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}AB//\;a\\AB = a\end{array} \right.\) và \(\overrightarrow {A'B'} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}A'B'\;//\;a\\A'B' = a\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}AB//\;A'B'\\AB = A'B'\end{array} \right.\)
Tương tự, ta cũng suy ra \(\left\{ \begin{array}{l}BC//\;B'C'\\BC = B'C'\end{array} \right.\)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c-g-c)
\(\left\{ \begin{array}{l}AC//\;A'C'\\AC = A'C'\end{array} \right.\)
Dễ dàng suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Cho các vectơ a → = 4 ; - 2 ; b → = - 1 ; - 1 ; c → = 2 ; 5 . Phân tích vectơ b → theo hai vectơ a → và c → , ta được:
A. b → = - 1 8 a → - 1 4 c →
B. b → = 1 8 a → - 1 4 c →
C. b → = - 1 2 a → - 4 c →
D. b → = - 1 8 a → + 1 4 c →
Cho hình vuông ABCD cạnh a túng các tích vô hướng a. Vectơ AB.AC b. vectơ AC.BD
a: ABCD là hình vuông
=>AC là phân giác của góc BAD và \(AC^2=AB^2+BC^2\)
AC là phân giác của góc BAD
=>\(\widehat{BAC}=\widehat{DAC}=\dfrac{1}{2}\cdot90^0=45^0\)
\(AC^2=AB^2+BC^2\)
=>\(AC^2=a^2+a^2=2a^2\)
=>\(AC=a\sqrt{2}\)
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB};\overrightarrow{AC}\right)\)
\(=a\cdot a\sqrt{2}\cdot cosBAC\)
\(=a^2\cdot\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=a^2\)
b: Vì ABCD là hình vuông
nên AC\(\perp\)BD
=>\(\overrightarrow{AC}\cdot\overrightarrow{BD}=0\)