Tìm tập xác định D của hàm số y = ( sin x + 2 ) / ( sin x . cos 2 x )
A. D = R \ k π 2 ; k ∈ Z
B. D = R \ π 2 + k π ; k ∈ Z
C. D = R \ π 2 + k 2 π ; k ∈ Z
D. D = R \ k π ; k ∈ Z
PB
Những câu hỏi liên quan
Tìm tập xác định D của hàm số
y
1
-
sin
x
1
+
sin
x
Đọc tiếp
Tìm tập xác định D của hàm số y = 1 - sin x 1 + sin x
Tìm tập xác định của hàm số \(y = \frac{1}{{\sin x}}\)
Biểu thức \(\frac{1}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
Đúng 0
Bình luận (0)
tìm tập xác định của hàm số sau :
y = sin(2x\x-1)
Hàm số xác định khi \(x-1\ne0\Leftrightarrow x\ne1\)
Đúng 0
Bình luận (0)
BT
7 tháng 12 2016 lúc 22:28
tìm tập xác định của hàm số : \(y=\frac{\sin\left(2x+5\right)}{\sin2x-\sin x}\)
Tìm tập xác định của các hàm số sau:
a) \(y = \frac{{1 - \cos x}}{{\sin x}}\);
b) \(y = \sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} .\)
a) Biểu thức \(\frac{{1 - \cos x}}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
b) Biểu thức \(\sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \) có nghĩa khi \(\left\{ {\begin{array}{*{20}{c}}{\frac{{1 + \cos x}}{{2 - \cos x}} \ge 0}\\{2 - \cos x \ne 0}\end{array}} \right.\)
Vì \( - 1 \le \cos x \le 1 ,\forall x \in \mathbb{R}\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\)
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số sau
y
c
o
t
x
2
.
sin
x
-
1
Đọc tiếp
Tìm tập xác định của hàm số sau y = c o t x 2 . sin x - 1
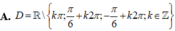
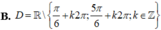
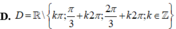
tìm tập xác định của hàm số sau đây:
a)\(y=sin^{x-1}_{x+2}\)
b)\(y=\sqrt{3-2cosx}\)
c)\(y=\sqrt{\dfrac{1+cosx}{1-cosx}}\)
ĐKXĐ:
a. Không hiểu đề bài là gì
b. \(3-2cosx\ge0\)
\(\Leftrightarrow cosx\le\dfrac{3}{2}\) (luôn đúng)
Vậy \(D=R\)
c. \(\left\{{}\begin{matrix}\dfrac{1+cosx}{1-cosx}\ge0\left(luôn-đúng\right)\\1-cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow cosx\ne1\Leftrightarrow x\ne k2\pi\)
Đúng 0
Bình luận (0)
tìm tập xác định của hàm số y= \(\sqrt{\sin x}\)
ĐK: sin(x) >= 0 mà -1 <=sin(x) <= 1 ;
nên TXĐ : 0 <= sin(x) <= 1
Đúng 0
Bình luận (0)
Tập xác định của hàm số y = sin(x + pi/4) là
1.Tìm tập xác định của hàm số: y= \(\sqrt{1+sinx-2cos^2x}\)
2. Cho hàm số: y = \(\sqrt{sin^4x+cos^4x-2msinx.cosx}\)
Tìm các giá trị của m để xác định với mọi x.
