Xét tính tăng giảm của các dãy số sau: u n = n - n 2 - 1
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
xét tính tăng, giảm của các dãy số sau
\(u_n=\dfrac{n+2}{n}\)
\(u_n=\dfrac{n+2}{n}\)
\(u_{n+1}=\dfrac{n+3}{n+1}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n+3}{n+1}-\dfrac{n+2}{n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n\left(n+3\right)-\left(n+1\right)\left(n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-\left(n^2+3n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-n^2-3n-2}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{-2}{n\left(n+1\right)}< 0\)
Vậy dãy số \(u_n\) đã cho là dãy giảm
Xét tính tăng giảm của các dãy số sau: u n = n + ( - 1 ) n n 2
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Xét tính tăng giảm và bị chặn của các dãy số sau: u 1 = 2 ; u 2 = 3 u n + 1 = u n + u n - 1 , ∀ n ≥ 2
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 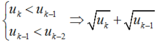
![]()
Vậy dãy (un) là dãy tăng và bị chặn.
Xét tính tăng , giảm của các dãy số \(\left(u_n\right)\) biết
\(u_n=\dfrac{\left(-1\right)^n}{n+2}\)
Lời giải:
Với $n$ lẻ bất kỳ:
$u_n<0; u_{n+1>0; u_{n+2}< 0$
$\Rightarrow u_n< u_{n+1}> u_{n+2}$ với mọi $n$ lẻ bất kỳ
Do đó dãy không tăng cũng không giảm.
Bài 1: Xét tính tăng giảm của các dãy số (Un) với
a)\(Un=\dfrac{2^n-1}{2^n+1}\) b)\(Un=\left(-1\right)^n.n\)
Bài 2: Xét tính bị chặn của
\(Un=\sqrt[3]{n}-\sqrt[3]{n+1}\)
xét tính tăng, giảm của các dãy số sau
a) \(u_n=2-3n\)
b) \(u_n=\dfrac{n+1}{n}\)
c) \(u_n=\dfrac{1}{n+1}\)
d) \(u_n=2^n\)
a: \(u_{n+1}-u_n\)
\(=2-3\left(n+1\right)-2+3n\)
=-3n-3+3n
=-3<0
=>Đây là dãy giảm
b: \(u_{n+1}-u_n\)
\(=\dfrac{n+2}{n+1}-\dfrac{n+1}{n}\)
\(=\dfrac{n^2+2n-n^2-2n-1}{n\left(n+1\right)}=\dfrac{-1}{n\left(n+1\right)}< 0\)
=>Đây là dãy giảm
c: \(u_{n+1}-u_n==\dfrac{1}{n+2}-\dfrac{1}{n+1}\)
\(=\dfrac{n+1-n-2}{\left(n+1\right)\left(n+2\right)}=\dfrac{-1}{\left(n+1\right)\left(n+2\right)}< 0\)
=>Đây là dãy giảm
d: \(\dfrac{u_{n+1}}{u_n}=\dfrac{2^{n+1}}{2^n}=2>1\)
=>Đây là dãy tăng
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 - n
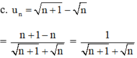
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
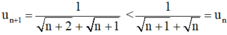
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
Xét tính tăng giảm của dãy số sau: \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{u_n^2+1}{4}\end{matrix}\right.\), n\(\ge\)1
Ta sẽ chứng minh \(\left(u_n\right)\) giảm, tức \(u_{n+1}< u_n\) (*) bằng phương pháp quy nạp.
Với n = 1: \(u_2-u_1=\dfrac{u_1^2+1}{4}-u_1=\dfrac{2^2+1}{4}-2=\dfrac{-3}{4}< 0\)
Giả sử (*) đúng với n = k (\(k\in N;k>1\)), tức \(u_{k+1}< u_k\)
Ta sẽ chứng minh (*) đúng với n = k + 1, tức \(u_{k+2}< u_{k+1}\)
\(u_{k+2}=\dfrac{\left(u_{k+1}\right)^2+1}{4}< \dfrac{u_k^2+1}{4}=u_{k+1}\)
Theo nguyên lí quy nạp, ta được đpcm.
Vậy \(\left(u_n\right)\) giảm.
Xét tính tăng giảm của dãy số: un = \(\dfrac{3^n-1}{2^n}\)
\(u_n=\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}=\dfrac{3^{n+1}-1}{2^{n+1}}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{3^{n+1}-1}{2^{n+1}}-\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{2^n.3^{n+1}-2^n-2^{n+1}.3^n+2^{n+1}}{2^n.2^{n+1}}\)
\(=\dfrac{2^n.3^n\left(3-2\right)-2^n\left(2-1\right)}{2^{2n+1}}\)
\(=\dfrac{2^n.\left(3^n-1\right)}{2^{2n+1}}\)
\(=\dfrac{\left(3^n-1\right)}{2}>0\left(n>1\right)\)
Vậy dãy \(u_n\)đã cho tăng