Đường thẳng y= 6x+m là tiếp tuyến của đường cong y = x 3 + 3 x - 1 khi m bằng
A. m = - 3 h o ặ c m = 1
B. m = 3 h o ặ c m = 1
C. m = 3 h o ặ c m = - 1
D. m = - 3 h o ặ c m = - 1
Đường thẳng y = 3x + m là tiếp tuyến của đường cong y = x 3 + 2 khi m bằng
A. 1 hoặc -1
B. 3 hoặc -3
C. 4 hoặc 0
D. 2 hoặc -2
Chọn C
y ' = 3 x 2 . Đường thẳng y = 3x + m là tiếp tuyến của đường cong y = x 3 + 2
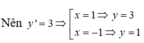
Tiếp tuyến của đường cong tại A(1;3) là y = 3(x - 1) + 3 hay y = 3x.
Tiếp tuyến của đường cong tại B(-1;1) là y = 3(x + 1) + 1 hay y = 3x + 4.
Do đó m ∈ {0; 4}
cho hàm số y=x^3-3x^3+2(C). viết pt tiếp tuyến của (C) a) Tại điểm có tung độ bằng 2 b) Tại điểm M mà tiếp tuyến tại M song song với đường thẳng y=6x+1
a:Sửa đề: y=x^3-3x^2+2
y'=3x^2-3*2x=3x^2-6x
y=2
=>x^3-3x^2=0
=>x=0 hoặc x=3
=>y'=0 hoặc y'=3*3^2-6*3=27-18=9
A(0;2); y'=0; y=2
Phương trình tiếp tuyến có dạng là;
y-2=0(x-0)
=>y=2
A(3;2); y'=9; y=2
Phương trình tiếp tuyến có dạng là:
y-2=9(x-3)
=>y=9x-27+2=9x-25
b: Tiếp tuyến tại M song song với y=6x+1
=>y'=6
=>3x^2-6x=6
=>x^2-2x=2
=>x=1+căn 3 hoặc x=1-căn 3
=>y=0 hoặc y=0
M(1+căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1-căn 3)=6x-6-6căn3
M(1-căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1+căn 3)
=>y=6x-6+6căn 3
Đường thẳng (d) :y=12x+m(m<0) là tiếp tuyến của đường cong (C):y=x3+2. Khi đó đường thẳng (d) cắt trục hoành và trục tung tại hai điểm A,B . Tính diện tích OAB
1. Cho đường tròn (c) : \(x^2+y^2+6x-2y=0\) và đường thẳng d : \(x-3y-4=0\)
Tính tiếp tuyến của (C) song song với (d)
2. Tìm giá trị của m để đường thẳng \(\Delta:3x+4y+3=0\) tiếp xúc với (C) : \(\left(x-m\right)^2+y^2=9\)
3. Xác đinh m để \(\left(C_m\right):x^2+y^2-4x+2\left(m+1\right)y+3m+7=0\) là phương trình của một đường tròn
1: x^2+y^2+6x-2y=0
=>x^2+6x+9+y^2-2y+1=10
=>(x+3)^2+(y-1)^2=10
=>R=căn 10; I(-3;1)
Vì (d1)//(d) nên (d1): x-3y+c=0
Theo đề, ta có: d(I;(d1))=căn 10
=>\(\dfrac{\left|-3\cdot1+1\cdot\left(-3\right)+c\right|}{\sqrt{1^2+\left(-3\right)^2}}=\sqrt{10}\)
=>|c-6|=10
=>c=16 hoặc c=-4
Có bao nhiêu điểm M thuộc đường cong (C): y = x + 1 x - 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng OM.
A. 3.
B. 2.
C. 1.
D. 4.
Có bao nhiêu điểm M thuộc đường cong C : y = x + 1 x - 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng OM.
A. 3.
B. 2.
C. 1.
D. 4.
1/ tìm tung độ giao điểm của đồ thị(C): \(\frac{2x-3}{x+3}\) và đường thẳng (d): y=x-1
2/ tiếp tuyến của đường cong(C) : y=x4+2x2 tại điểm M(1;3) có phương trình là
3/ đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số y=x3 -3x2+1 có phương trình là
1.
Pt hoành độ giao điểm: \(\frac{2x-3}{x+3}=x-1\)
\(\Leftrightarrow2x-3=x^2+2x-3\)
\(\Leftrightarrow x=0\Rightarrow y=-1\)
Vậy tung độ giao điểm là \(-1\)
2.
\(y'=4x^3+4x\Rightarrow\left\{{}\begin{matrix}y'\left(1\right)=8\\y\left(1\right)=3\end{matrix}\right.\)
Pttt: \(y=8\left(x-1\right)+3=8x-5\)
3.
\(y'=3x^2-6x\)
Lấy y chia y' và lấy phần dư ta được pt đường thẳng là: \(y=-2x+1\)
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = 2 x + 4 x − 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng:
A. 2
B. -1
C. -2
D. 1
Đáp án D
Ta có
x + 1 = 2 x + 4 x − 1 ⇒ x 2 − 2 x − 5 = 0 ⇒ x 1 = x M + x N 2 = x 1 + x 2 2 = 2 2 = 1
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = 2 x + 4 x − 1 Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. x = -1
B. x=1
C. x= - 2
D. x= 2
Đáp án B
PT hoành độ giao điểm là
x + 1 = 2 x + 4 x − 1 ⇔ x ≠ 1 x 2 − 2 x − 5 = 0 x M + x N = 2 ⇒ x 1 = x M + x N 2 = 1