Đặt \(\sqrt{x-1}+\sqrt{5-x}=t\)

\(t\ge\sqrt{x-1+5-x}=2\)

\(t\le\sqrt{2\left(x-1+5-x\right)}=2\sqrt{2}\)

\(t^2=4+2\sqrt{\left(x-1\right)\left(5-x\right)}\Rightarrow\sqrt{\left(x-1\right)\left(5-x\right)}=\dfrac{t^2-4}{2}\)

Pt trở thành:

\(t+\dfrac{3\left(t^2-4\right)}{2}=m\Leftrightarrow\dfrac{3}{2}t^2+t-6=m\)

Xét hàm \(f\left(t\right)=\dfrac{3}{2}t^2+t-6\) với \(t\in\left[2;2\sqrt{2}\right]\)

\(-\dfrac{b}{2a}=-\dfrac{1}{3}\notin\left[2;2\sqrt{2}\right]\)

\(f\left(2\right)=2\) ; \(f\left(2\sqrt{2}\right)=6+2\sqrt{2}\) \(\Rightarrow2\le f\left(t\right)\le6+2\sqrt{2}\)

\(\Rightarrow\) Pt có nghiệm khi \(2\le m\le6+2\sqrt{2}\)

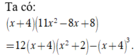
Khi đó phương trình đã cho trở thành 

Để phương trình đã cho có bốn nghiệm thực phân biệt ⇔  phương trình (2) có hai nghiệm phân biệt thuộc (1;3)

có 4 giá trị nguyên m thỏa. Chọn A.

⇔ x − 1 ≥ 0 2 x + m = x − 1 2 ⇔ x ≥ 1 x 2 − 4 x + 1 − m = 0     ( * )

Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất.

TH1:  ∆ ' = 0 ⇔ m = - 3 thì (*) có nghiệm kép  x = 2 ≥ 1 (thỏa).

TH2:  ∆ ' > 0 ⇔ m > - 3 thì phương trình có nghiệm duy nhất khi (*) có 2 nghiệm thỏa mãn:

x 1 < 1 < x 2 ⇔ x 1 - 1 x 2 - 1 < 0 ⇔ x 1 x 2 - x 1 + x 2 + < 0

⇔ 1 - m - 4 + < 0 ⇔ m > - 2

Do m không dương nên m ∈ {−1; 0}

Kết hợp với trường hợp m = −3 ở trên ta được 3 giá trị của m thỏa mãn bài toán.

Đáp án cần chọn là: B

Đáp án C

Chọn C

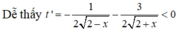
nên hàm t = t (x) nghịch biến trên (-2;2)

Thay vào bất phương trình trên được:

Bất phương trình đã cho nghiệm đúng với mọi x ∈ - 2 ; 2  nếu và chỉ nếu bất phương trình

nghiệm đúng với mọi  t ∈ - 6 ; 2

tam thức bậc hai f t = 2 t 2 - m t + 3 m - 5 có hai nghiệm thỏa mãn

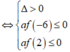
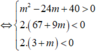
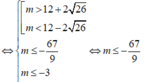
Kết hợp với m ∈ - 10 ; 10   thì  m ∈ - 10 ; - 9 ; - 8

Đáp án là A

1B

2A

Đáp án D.

Ta có:

P T ⇔ m 9 4 x − 2 m + 1 6 4 x + m ≤ 0 ⇔ m 3 2 2 x − 2 m + 1 3 2 x + m ≤ 0

Đặt t = 3 2 x ;  do x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .  Khi đó PT trở thành: m t 2 − 2 m + 1 t + m ≤ 0 ⇔ m t 2 − 2 t + 1 ≤ t

Rõ ràng t = 1 là nghiệm của BPT đã cho.

Với t ∈ 1 ; 3 2 ⇒ m ≤ t t − 1 2 = f t ,  xét f x  với t ∈ 1 ; 3 2  ta có:

f ' t = t − 1 − 2 t t − 1 3 = − t − 1 t − 1 2 < 0 ∀ t ∈ 1 ; 3 2

do đó f t   nghịch biến trên 1 ; 2 3 .

Do đó BPT nghiệm đúng vơi ∀ t ∈ 1 ; 3 2 ⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6

Vậy có 6 giá trị nguyên dương của m thỏa mãn.