Cho ba vecto a → , b → , c → trong không gian. Chứng minh rằng nếu m a → + n b → + p c → = 0 → và một trong ba số m, n, p khác không thì ba vecto a → , b → , c → đồng phẳng
PB
Những câu hỏi liên quan
Cho hình hộp ABCDA'B'C'D" .Gọi điểm M thuộc các đường thẳng A'C sao cho vecto MA =-3 vecto MC . Đặt vecto BA= vecto a,vecto BB'= vecto b ,vectoBC =vecto c . Hãy biểu thị vecto BM qua các vecto a,b,c
Cho hai vecto
a
→
và
b
→
đều khác vecto
0
. Hãy xác định vecto
c
→
2
a
→
-
b
→
và giải thích tại sao ba vecto
a
→
,
b...
Đọc tiếp
Cho hai vecto a → và b → đều khác vecto 0 . Hãy xác định vecto c → = 2 a → - b → và giải thích tại sao ba vecto a → , b → , c → đồng phẳng
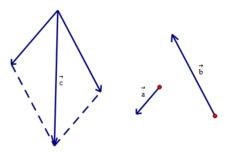
a → , b → , c → đồng phẳng vì a → và b → không cùng phương và có cặp số (2; -1) sao cho c → = 2 a → - b →
Đúng 0
Bình luận (0)
Trong không gian cho ba vecto tùy ý
a
→
,
b
→
,
c
→
Gọi
u
→
a
→
− 2
b
→
,
v
→
3
b
→
−
c...
Đọc tiếp
Trong không gian cho ba vecto tùy ý a → , b → , c →
Gọi u → = a → − 2 b → , v → = 3 b → − c → , w → = 2 c → − 3 a →
Chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng.
Muốn chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng ta cần tìm hai số thực p và q sao cho w → = p u → + q v →
Giả sử có w → = p u → + q v →
2 c → – 3 a → = p( a → – 2 b → ) + q(3 b → − c → )
⇔ (3 + p) a → + (3q − 2p) b → − (q + 2) c → = 0 → (1)
Vì ba vecto lấy tùy ý a → , b → , c → nên đẳng thức (1) xảy ra khi và chỉ khi:
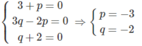
Như vậy ta có: w → = −3 u → − 2 v → nên ba vecto u → , v → , w → đồng phẳng.
Đúng 0
Bình luận (0)
Cho ba vecto
a
→
,
b
→
,
c
→
. Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng. A. Một trong ba vecto đó bằng
0
→
. B. Có hai trong ba vecto đó cùng phương. C. Có một vecto không cùng hướng với hai vecto còn lại D. Có hai trong ba vecto đó cùng hướng.
Đọc tiếp
Cho ba vecto a → , b → , c → . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.
A. Một trong ba vecto đó bằng 0 → .
B. Có hai trong ba vecto đó cùng phương.
C. Có một vecto không cùng hướng với hai vecto còn lại
D. Có hai trong ba vecto đó cùng hướng.
Nếu hai trong ba vecto đó cùng hướng thì ba vecto đồng phẳng; nếu hai trong ba vecto đó không cùng hướng thì chưa thể kết luận được ba vecto đó đồng phẳng.
Đáp án C
Đúng 0
Bình luận (0)
Cho ba vecto
a
→
,
b
→
,
c
→
. Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng? A. Một trong ba vecto đó bằng
0
→
B. Có hai trong ba vecto đó cùng phương C. Có một vecto không cùng hướng với hai vecto còn lại. D. Có hai trong ba vecto đó cùng hướng
Đọc tiếp
Cho ba vecto a → , b → , c → . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng?
A. Một trong ba vecto đó bằng 0 →
B. Có hai trong ba vecto đó cùng phương
C. Có một vecto không cùng hướng với hai vecto còn lại.
D. Có hai trong ba vecto đó cùng hướng
Bài 1: Cho năm điểm bất kì A, B, C, D, E. CMR:
Vecto AB + vecto DE - vecto DB + vecto BC Vecto AC + BE
Bài 2: Chó sáu điểm bất kì A, B, C, D, E, F. CMR:
a) Vecto AD + vecto BE + vecto CF Vecto AE + Vecto BF + vecto CD
b) Vecto AB + vecto CD Vecto AD + vecto CB
c)Vecto AB - vecto CD Vecto AB - vecto BD
Bài 3: Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm và I là trung điểm của BC. Vẽ đường kính AK. CMR: Vecto IH + vecto IB + vecto IK + vecto IC Vecto 0
Bài 4: Cho h...
Đọc tiếp
Bài 1: Cho năm điểm bất kì A, B, C, D, E. CMR:
Vecto AB + vecto DE - vecto DB + vecto BC = Vecto AC + BE
Bài 2: Chó sáu điểm bất kì A, B, C, D, E, F. CMR:
a) Vecto AD + vecto BE + vecto CF = Vecto AE + Vecto BF + vecto CD
b) Vecto AB + vecto CD = Vecto AD + vecto CB
c)Vecto AB - vecto CD = Vecto AB - vecto BD
Bài 3: Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm và I là trung điểm của BC. Vẽ đường kính AK. CMR: Vecto IH + vecto IB + vecto IK + vecto IC = Vecto 0
Bài 4: Cho hình bình hành ABCD với O là tâm. CMR:
a) Vecto CO - vecto OB = Vecto BA
b) Vecto AB - vecto BC = Vecto DB
c) Vecto DA - vecto DB = Vecto OD - vecto OC
d) Vecto DA - vecto DB + vecto DC = Vecto 0
Bài 4: Cho tam giác ABC vuông cân tại A, trọng tâm G. cạnh AB=a. Gọi I là trung điểm BC. Tính độ dài vecto sau:
a) Vecto a= vecto AB + vecto AC
b) Vecto b= vecto AB + vecto AC + vecto AG
c) Vecto c= vecto BA + vecto BC
d) Vecto d= vecto AB - vecto AC + vecto BI
1) Ta có:\(\overrightarrow{AB}+\overrightarrow{DE}-\overrightarrow{DB}+\overrightarrow{BC}=\overrightarrow{AE}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{BE}+\overrightarrow{EC}\)
\(=\overrightarrow{AC}+\overrightarrow{BE}+\overrightarrow{CE}+\overrightarrow{EC}=\overrightarrow{AC}+\overrightarrow{BE}\left(đpcm\right)\)2) a) Ta có: \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\left(đpcm\right)\)
b) Ta có: \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)
\(=\overrightarrow{AD}+\overrightarrow{CB}+\overrightarrow{DB}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{CB}\left(đpcm\right)\)c) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AB}-\overrightarrow{BD}\)
\(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}+\overrightarrow{BC}\) ( đề bài bị lỗi gì à ?? :v ) hay do mình =))
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(Câu 1: Cho ba vecto a, b và c khác vecto - không. Trong các khẳng định sau, khẳng định nào saiA. a + b b + aB. ( a + b ) + c a + ( b + c )C. a + 0 aD. 0 + a 0Câu 2: Cho hình bình hành ABCD. Vecto tổng CB + CD bằngA. CAB. BDC. ACD. DBCâu 3: cho ba điểm phân biệt A , B , C. Trong các khẳng định sai khẳng định nào saiA. AB + BC ACB. AC + CB ABC. CA + BC BAD. CB + AC BACâu 4: Cho bốn điểm A,B,C,D . Vecto tổng AB + CD + BC + Da bằngA. 0B. ACC. BDD. BA
Đọc tiếp
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(
Câu 1: Cho ba vecto a, b và c khác vecto - không. Trong các khẳng định sau, khẳng định nào sai
A. a + b = b + a
B. ( a + b ) + c = a + ( b + c )
C. a + 0 = a
D. 0 + a = 0
Câu 2: Cho hình bình hành ABCD. Vecto tổng CB + CD bằng
A. CA
B. BD
C. AC
D. DB
Câu 3: cho ba điểm phân biệt A , B , C. Trong các khẳng định sai khẳng định nào sai
A. AB + BC = AC
B. AC + CB = AB
C. CA + BC = BA
D. CB + AC = BA
Câu 4: Cho bốn điểm A,B,C,D . Vecto tổng AB + CD + BC + Da bằng
A. 0
B. AC
C. BD
D. BA
Câu 1: B
Câu 2: A
Câu 3: D
Câu 4: A
Đúng 1
Bình luận (0)
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(Câu 1: Cho ba vecto a, b và c khác vecto - không. Trong các khẳng định sau, khẳng định nào saiA. a + b b + aB. ( a + b ) + c a + ( b + c )C. a + 0 aD. 0 + a 0Câu 2: Cho hình bình hành ABCD. Vecto tổng CB + CD bằngA. CAB. BDC. ACD. DBCâu 3: cho ba điểm phân biệt A , B , C. Trong các khẳng định sai khẳng định nào saiA. AB + BC ACB. AC + CB ABC. CA + BC BAD. CB + AC BACâu 4: Cho bốn điểm A,B,C,D . Vecto tổng AB + CD + BC + Da bằngA. 0B. ACC. BDD. Ba
Đọc tiếp
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(
Câu 1: Cho ba vecto a, b và c khác vecto - không. Trong các khẳng định sau, khẳng định nào saiA. a + b = b + aB. ( a + b ) + c = a + ( b + c )C. a + 0 = aD. 0 + a = 0Câu 2: Cho hình bình hành ABCD. Vecto tổng CB + CD bằngA. CAB. BDC. ACD. DBCâu 3: cho ba điểm phân biệt A , B , C. Trong các khẳng định sai khẳng định nào saiA. AB + BC = ACB. AC + CB = ABC. CA + BC = BAD. CB + AC = BACâu 4: Cho bốn điểm A,B,C,D . Vecto tổng AB + CD + BC + Da bằngA. 0B. ACC. BDD. BaCâu 1: B
Câu 2: A
Câu 3: D
Câu 4: A
Đúng 1
Bình luận (0)
Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương hay không?
b) Ngược lại, nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.
Đúng 0
Bình luận (0)




