Giải phương trình: x2 – 4x = (-1)/2.
PB
Những câu hỏi liên quan
Cho phương trình ẩn x : x2 - 4x + m -1 =0 (1)
a) Giải phương trình (1) với m = -4
b) Với x1,x2 là nghiệm phương trình (1). Tìm giá trị của m, biết x1-x2= 2
Giải các phương trình sau: (2 x 2 + 1)(4x – 3) = (2 x 2 + 1)(x – 12)
Giải phương trình: x 2 – 4 x = ( - 1 ) / 2 .
x 2 − 4 x = ( − 1 ) / 2 ⇔ x 2 − 4 x + 4 = ( − 1 ) / 2 + 4 ⇔ ( x − 2 ) 2 = 7 / 2 ⇔ x − 2 = ± ( 7 / 2 ) ⇔ x = 2 ± ( 7 / 2 )
Vậy phương trình có hai nghiệm: x 1 = 2 + √ ( 7 / 2 ) ; x 2 = 2 - √ ( 7 / 2 )
Đúng 0
Bình luận (0)
Cho phương trình: x2- 4x + m +1 = 0 (1)
1) Giải phương trình (1) khi m = 2.
2) Tìm giá trị của m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn đẳng thức \(x_1^2+x_2^2\)= 5 (x1 + x2)
a,Thay m=2 vào pt :
\(\left(1\right)\Leftrightarrow x^2-4x+3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
b, Để pt có 2 nghiệm thì \(\Delta'\ge0\)
\(\Leftrightarrow\left(-2\right)^2-1\left(m+1\right)\ge0\\ \Leftrightarrow4-m-1\ge0\\ \Leftrightarrow3-m\ge0\\ \Leftrightarrow m\le3\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m+1\end{matrix}\right.\)
\(x^2_1+x^2_2=5\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5.4\\ \Leftrightarrow4^2-2\left(m+1\right)=20\\ \Leftrightarrow16-2m-2-20=0\\ \Leftrightarrow m=-3\left(tm\right)\)
Đúng 1
Bình luận (0)
a)Thay \(m=2\) vào (1) ta đc:
\(x^2-4x+2+1=0\Rightarrow x^2-4x+3=0\)
\(\Rightarrow\left(x-3\right)\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
b)Áp dụng hệ thức Viet:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{4}{1}=4\\x_1\cdot x_2=\dfrac{c}{a}=m+1\end{matrix}\right.\) (*)
Theo bài: \(x_1^2+x^2_2=5\left(x_1+x_2\right)\)
\(\Rightarrow\left(x_1+x_2\right)^2-2x_1\cdot x_2=5\left(x_1+x_2\right)\)
\(\Rightarrow4^2-2\cdot\left(m+1\right)=5\cdot4\)
\(\Rightarrow m=-1\)
Đúng 0
Bình luận (1)
Giải phương trình (x2+x+1)2=(4x-1)2
\(\left(x^2+x+1\right)^2=\left(4x-1\right)^2\)
\(\Leftrightarrow\left(x^2+x+1\right)^2-\left(4x-1\right)^2=0\)
\(\Leftrightarrow\left[\left(x^2+x+1\right)-\left(4x-1\right)\right]\left[\left(x^2+x+1\right)+\left(4x-1\right)\right]=0\)
\(\Leftrightarrow\left(x^2+x+1-4x+1\right)\left(x^2+x+1+4x-1\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(x^2+5x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-1=0\\x+5=0\\x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=-5\\x=0\end{matrix}\right.\)
Vậy: \(S=\left\{2;1;-5;0\right\}\)
Đúng 1
Bình luận (0)
Giải phương trình: (4x + 2)(x2 + 1) = 0
(4x + 2)(x2 + 1) = 0
⇔ 4x + 2 = 0 hoặc x2 + 1 = 0
+ 4x + 2 = 0 ⇔ 4x = -2 ⇔ x = 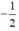
+ x2 + 1 = 0 ⇔ x2 = -1 (Phương trình vô nghiệm vì x2 ≥ 0 với mọi x ).
Vậy phương trình có tập nghiệm 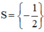
Đúng 0
Bình luận (0)
Giải các phương trình:
4
x
+
1
-
x
2
-
x
+
2
x
+
1
x
+
2
Đọc tiếp
Giải các phương trình: 4 x + 1 = - x 2 - x + 2 x + 1 x + 2
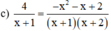
Điều kiện xác định: x ≠ -1; x ≠ -2.
Quy đồng và khử mẫu ta được:
4.(x + 2) = -x2 – x + 2
⇔ 4x + 8 = -x2 – x + 2
⇔ 4x + 8 + x2 + x – 2 = 0
⇔ x2 + 5x + 6 = 0.
Có a = 1; b = 5; c = 6 ⇒ Δ = 52 – 4.1.6 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt:
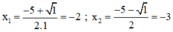
Chỉ có nghiệm x2 = -3 thỏa mãn điều kiện xác định.
Vậy phương trình có nghiệm x = -3.
Đúng 0
Bình luận (0)
Giải phương trình: ( x 2 - 1 ) ( x 2 + 4 x + 3 ) = - 3
Giải hệ phương trình:
phương trình 1:x2-5y2-8y=3
phương trình 2:(2x+4y-1)√(2x-y-1)=(4x-2y-3)√(x+2y)








