Trong C, phương trình z 2 - z + 1 = 0 có tổng hai nghiệm là:
A. -1
B. 1
C. i
D. –i
PB
Những câu hỏi liên quan
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
. Nếu
z
1
−
i
và
z
1
là hai nghiệm của phương trình thì
a
−
b
−
c
bằng (a, b, c là số thực). A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 . Nếu z = 1 − i và z = 1 là hai nghiệm của phương trình thì a − b − c bằng (a, b, c là số thực).
A. 2
B. 3
C. 5
D. 6
Phương trình z 2 + a z + b = 0 có một nghiệm phức là z = 1 + 2 i . Tổng 2 số a và b bằng:
A. 0
B. -3
C. 3
D. -4
Chọn C
Vì z = 1 + 2i là một nghiệm của phương trình z2 + az + b = 0 nên ta có:
Đúng 0
Bình luận (0)
Phương trình
z
2
+
a
z
+
b
0
có một nghiệm phức là
z
1
+
2
i
.
Tổng 2 số a và b bằng: A. 0 B. -3 C. 3 D. -4
Đọc tiếp
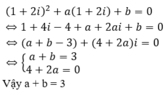
Phương trình z 2 + a z + b = 0 có một nghiệm phức là z = 1 + 2 i . Tổng 2 số a và b bằng:
A. 0
B. -3
C. 3
D. -4
Chọn C.
Vì z = 1 + 2i là một nghiệm của phương trình z2 + az + b = 0 nên ta có:
Đúng 0
Bình luận (0)
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
Nếu z1-i và z1 là 2 nghiệm của phương trình thì
a
-
b
-
c
bằng A. 2 B. 3 C. 5 D. 6
Đọc tiếp
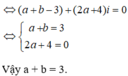
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Cho phương trình: x²-2(m-3)x+(m-4)=0 (1) a) giải phương trình với m=1 b) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt c) Xác định m để phương trình có hai nghiệm trái dấu d)Tính theo m giá trị của biểu thức A=1/x1+1/x2.Tìm m để A € Z để A € Z
a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4
Đúng 0
Bình luận (0)
Phương trình
z
2
+
az
+
b
0
,
a
,
b
∈
ℝ
có một nghiệm phức là
z
1
+
2
i
. Khi đó tổng
a
+
b
bằng A. -4 B. 3 C. 0 D. -3
Đọc tiếp
Phương trình z 2 + az + b = 0 , a , b ∈ ℝ có một nghiệm phức là z = 1 + 2 i . Khi đó tổng a + b bằng
A. -4
B. 3
C. 0
D. -3
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
nhận
z
2
và
z
1
+
i
làm các nghiệm của phương trình. Khi đó
a
-
b
+
c
là
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
Trong C, phương trình z2 - z + 1 0 có nghiệm là: A. B. C. D.
Đọc tiếp
Trong C, phương trình z2 - z + 1 = 0 có nghiệm là:
A.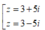 
B.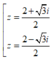 
C.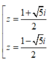 
D.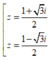 
Chọn D.
Nên phương trình có hai nghiệm phức là:
Đúng 0
Bình luận (0)
Trong C, phương trình
z
2
-
z
+
1
0
có nghiệm là: A.
z
3
+
5
i
h
o
ặ
c
z
3
-
5
i
B.
z
2
+
3
i...
Đọc tiếp
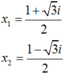
Trong C, phương trình z 2 - z + 1 = 0 có nghiệm là:
A. z = 3 + 5 i h o ặ c z = 3 - 5 i
B. z = 2 + 3 i 2 h o ặ c z = 2 - 3 i 2
C. z = 1 + 5 i 2 h o ặ c z = 1 - 5 i 2
D. z = 1 + 3 i 2 h o ặ c z = 1 - 3 i 2
