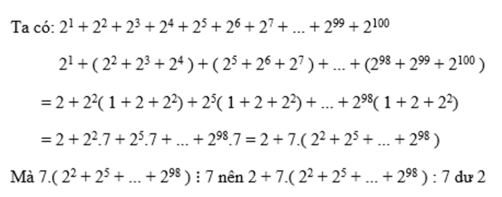Tìm số dư khi chia A=1+2+22+23+.....+22005 cho 7
NT
Những câu hỏi liên quan
cho A=1+2+22+23+.....+241
a) Thu gọn tổng A
b) chứng tỏ rằng:a chia hết cho 3,7
c)tìm số dư của a khi chia cho 5
a: \(A=1+2+2^2+...+2^{41}\)
=>\(2A=2+2^2+2^3+...+2^{42}\)
=>\(2A-A=2^{42}-1\)
=>\(A=2^{42}-1\)
b: \(A=\left(1+2\right)+2^2\left(1+2\right)+...+2^{40}\left(1+2\right)\)
\(=3\left(1+2^2+...+2^{40}\right)⋮3\)
\(A=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{39}\left(1+2+2^2\right)\)
\(=7\left(1+2^3+...+2^{39}\right)⋮7\)
Đúng 1
Bình luận (0)
Cho A = 1 + 2 + 2 2 + . . . + 2 2009 + 2 2010 . Tìm số dư khi chia A cho 7
Ta có: A = 1 + 2 + 2 2 + . . . + 2 2009 + 2 2010
= 1 + 2 ( 1 + 2 + 2 2 ) + ... + 2 2008 ( 1 + 2 + 2 2 )
= 1 + 2 ( 1 + 2 + 4 ) + ... + 22008 ( 1 + 2 + 4 )
= 1 + 2 . 7 + ... + 2 2008 . 7 = 1 + 7 ( 2 + ... + 2 2008 )
Mà 7 ( 2 + ... + 2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.
Đúng 0
Bình luận (0)
Cho A = 1 + 2 + 2 2 + ... + 2 2009 + 2 2010 . Tìm số dư khi chia A cho 7.
Ta có: A = 1 + 2 + 2 2 + 2 3 + ... + 2 2008 + 2 2009 + 2 2010
= 1 + 2 ( 1 + 2 + 22 ) + ... + 2 2008 ( 1 + 2 + 22 )
= 1 + 2 ( 1 + 2 + 4 ) + ... + 2 2008 ( 1 + 2 + 4 )
= 1 + 2 . 7 + ... + 2 2008 . 7 = 1 + 7 ( 2 + ... + 2 2008 )
Mà 7 ( 2 + ... + 2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.
Đúng 0
Bình luận (0)
Tính S= 1/22+1/23+...+1/22005
\(S=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2005}}\)
\(2.S=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\)
\(2.S-S=\left(2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\)
\(S=2-\dfrac{1}{2^{2006}}\)
Đúng 2
Bình luận (0)
A=20+21+22+23+24+.........+22015+22016
Tìm số dư khi chia A cho 7.![]()
A=(1+2+2^2)+2^3(1+2+2^2)+...+2^2013(1+2+2^2)+2^2016
=7(1+2^3+...+2^2013)+2^2016
Vì 2^2016 chia 7 dư 1
nên A chia 7 dư 1
Đúng 0
Bình luận (0)
Tìm số dư khi chia
1 + 2 + 22+ 23+ ... + 2100 chia cho 3
\(A=1+2+2^2+2^3+...+2^{100}\)
\(=1+\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\)
\(=1+2\left(1+2\right)+2^3\left(1+2\right)+...+2^{99}\left(1+2\right)\)
\(=1+3\left(2+2^3+...+2^{99}\right)\)
=>A chia 3 dư 1
Đúng 2
Bình luận (0)
Tìm dư của phép chia số A = 22021 + 22022 chia cho B = 1 + 2 + 22 + 23 +....+22016 + 22017
Tính số dư khi chia:
( 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 ) cho 7
Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2
Đúng 0
Bình luận (0)
Tính số dư khi chia:
( 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 ) cho 7
Tìm số dư trong phép chia 2 2014 cho
1 + 2 + 2 2 + 2 3 + . . . + 2 2011