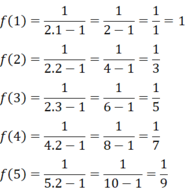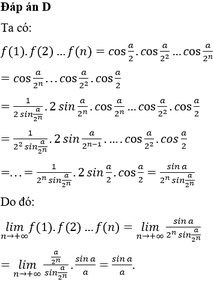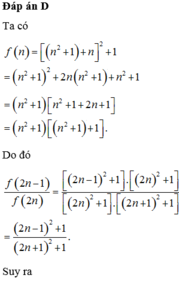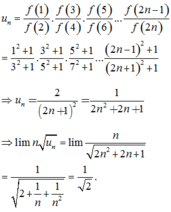Viết thuật toán tính dãy Fibonacci: F1=1,F2=1 Fn= Fn-1+Fn-2 Nêu ý tưởng
TT
Những câu hỏi liên quan
1 VTC pascal nhập số nguyên n. Tính các số Fibonacci theo công thức: F1 F2 1; Fn F1 - 1 + F2 + 2 + Xuất dãy số Fibbonacci ra màn hình +Tính tống dãy số Fibonacci và xét tổng đó có phải là số nguyên tố k
Bài 2
VCt pascal nhập dãy số n(n từ bàn phím + Xuất ra màn hình số nhỏ nhất và số lớn nhất và tb cộng của dãy số...
Đọc tiếp
1 VTC pascal nhập số nguyên n. Tính các số Fibonacci theo công thức: F1 = F2 = 1; Fn = F1 - 1 + F2 + 2 + Xuất dãy số Fibbonacci ra màn hình +Tính tống dãy số Fibonacci và xét tổng đó có phải là số nguyên tố k Bài 2 VCt pascal nhập dãy số n(n từ bàn phím + Xuất ra màn hình số nhỏ nhất và số lớn nhất và tb cộng của dãy số + Kiểm tra giá trị tb đó có phải là số hoàn hảo không
Bài 1:
uses crt;
var f:array[1..255]of integer;
i,n,t,kt:integer;
begin
clrscr;
write('Nhap n='); readln(n);
i:=2;
f[1]:=1;
f[2]:=1;
repeat
i:=i+1;
f[i]:=f[i-1]+f[i-2];
until i=n;
writeln('Day so fibonaci la: ');
for i:=1 to n do
write(f[i]:4);
writeln;
t:=0;
for i:=1 to n do
t:=t+f[i];
writeln('Tong cua day la: ',t);
kt:=0;
for i:=2 to trunc(sqrt(t)) do
if t mod i=0 then kt:=1;
if (kt=0) and (t>1) then writeln(t,' la so nguyen to')
else writeln(t,' khong la so nguyen to');
readln;
end.
Đúng 0
Bình luận (0)
Bài 2:
uses crt;
var a:array[1..100]of integer;
i,n,max,min,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
max:=a[1];
min:=a[1];
for i:=1 to n do
begin
if max<a[i] then max:=a[i];
if min>a[i] then min:=a[i];
end;
t:=0;
for i:=1 to n do
t:=t+a[i];
writeln('So nho nhat la: ',min);
writeln('So lon nhat la: ',max);
writeln('Trung binh cong cua day so la: ',t/n:4:2);
readln;
end.
Đúng 0
Bình luận (0)
Cho hàm số f n = 1 2 n - 1 , n ∈ N*. Tính f 1 , f 2 , f 3 , f 4 , f 5 .
a) Nhập vào hai số nguyên a và b (1≤ a,b ≤ 109). Tính và in lên màn hình ước chung lớn nhất(UCLN) v à bội chung nhỏ nhất (BCNN) của a,b.b)Dãy số fibonacy được định nghĩa như sau:f1f21fnfn-1+fn-2 (với n 3)Hãy viết chương trình in ra n số đầu tiên của dãy fibonacy.Dữ liệu nhập:là số nguyên n (1n30)Dự liệu xuất: là n số fibonacy đầu tiên trên cùng một dòng, mỗi số cách nhau một khoảng trắng.
Đọc tiếp
a) Nhập vào hai số nguyên a và b (1≤ a,b ≤ 109). Tính và in lên màn hình ước chung lớn nhất(UCLN) v à bội chung nhỏ nhất (BCNN) của a,b.
b)Dãy số fibonacy được định nghĩa như sau:
f1=f2=1
fn=fn-1+fn-2 (với n >=3)
Hãy viết chương trình in ra n số đầu tiên của dãy fibonacy.
Dữ liệu nhập:là số nguyên n (1<=n<=30)
Dự liệu xuất: là n số fibonacy đầu tiên trên cùng một dòng, mỗi số cách nhau một khoảng trắng.
a)
program UCLN_va_BCNN;
uses crt;
var a,b,c,r,p:integer;
begin
clrscr;
write('nhap a,b:');readln(a,b);
if a<b then
begin
c:=a;
a:=b;
b:=c;
end;
p:=a*b;
r:=a mod b;
while r<>0 do
begin
a:=b;
b:=r;
r:=a mod b;
end;
writeln('UCLN la: ',b);
writeln('BCNN la: ',p div b);
readln;
end.
Đúng 0
Bình luận (0)
b)
program fibonaci;
uses crt;
var i,n:integer;
a:array[1..30]of integer;
begin
clrscr;
repeat
write('nhap n:');readln(n);
if (n<1)or(n>30) then writeln('so n phai lon hon hoac bang 1 va nho hon hoac bang 30:);
until (n>=1)and(n<=30);
a[1]:=1;
a[2]:=1;
for i:=3 to n do
a[i]:=a[i-1]+a[i-2];
writeln(n,' so fibonaci dau tien la:');
for i:=1 to n do
write(a[i]:3);
readln;
end.
Đúng 0
Bình luận (0)
Cho hàm số
f
n
cos
a
2
n
,
a
≠
0
,
n
∈
N
.
Tính giới hạn
l
i
m
n
→
+...
Đọc tiếp
Cho hàm số f n = cos a 2 n , a ≠ 0 , n ∈ N . Tính giới hạn l i m n → + ∞ ( 1 ) . f 2 . . . f n .
A. sin a 2 a
B. 2 sin a a
C. sin 2 a 2 a
D. sin a a
Đặt
f
n
n
2
+
n
+
1
2
+
1
. Xét dãy số
u
n
sao cho
u
n
f
1
....
Đọc tiếp
Đặt f n = n 2 + n + 1 2 + 1 . Xét dãy số u n sao cho u n = f 1 . f 3 . f 5 ... f 2 n − 1 f 2 . f 4 . f 6 ... f 2 n . Tính lim n u n
A. lim n u n = 2
B. lim n u n = 1 3
C. lim n u n = 3
D. lim n u n = 1 2
Đặt
f
n
n
2
+
n
+
1
2
+
1
. Xét dãy số
u
n
sao cho
u
n
f
1...
Đọc tiếp
Đặt f n = n 2 + n + 1 2 + 1 . Xét dãy số u n sao cho u n = f 1 . f 3 . f 5 ... f 2 n − 1 f 2 . f 4 . f 6 ... f 2 n . Tính lim n u n
A. lim n u n = 2
B. lim n u n = 1 3
C. lim n u n = 3
D. lim n u n = 1 2
Đáp án D
Ta có
f n = n 2 + 1 + n 2 + 1 = n 2 + 1 2 + 2 n n 2 + 1 + n 2 + 1
= n 2 + 1 n 2 + 1 + 2 n + 1 = n 2 + 1 n 2 + 1 + 1 .
Do đó
f 2 n − 1 f 2 n = 2 n − 1 2 + 1 . 2 n 2 + 1 2 n 2 + 1 . 2 n + 1 2 + 1 = 2 n − 1 2 + 1 2 n + 1 2 + 1 .
Suy ra
u n = f 1 f 2 . f 3 f 4 . f 5 f 6 ... f 2 n − 1 f 2 n = 1 2 + 1 3 2 + 1 . 3 2 + 1 5 2 + 1 . 5 2 + 1 7 2 + 1 ... 2 n − 1 2 + 1 2 n + 1 2 + 1
⇒ u n = 2 2 n + 1 2 = 1 2 n 2 + 2 n + 1
⇒ lim n u n = lim n 2 n 2 + 2 n + 1 = 1 2 + 1 n + 1 n 2 = 1 2 .
Đúng 0
Bình luận (0)
Trên một dây có sóng dừng mà các tần số trên dây theo quy luật:
f
1
:
f
2
:
f
3
:
...
:
f
n
1
:
2
:
3
:
...
:
n
. Trên dây thì A. số nút bằng số bụng trừ 1. B. số nút bằng số bụng cộng 1. C. số nút bằng số bụng. D. số nút bằng...
Đọc tiếp
Trên một dây có sóng dừng mà các tần số trên dây theo quy luật: f 1 : f 2 : f 3 : ... : f n = 1 : 2 : 3 : ... : n . Trên dây thì
A. số nút bằng số bụng trừ 1.
B. số nút bằng số bụng cộng 1.
C. số nút bằng số bụng.
D. số nút bằng số bụng trừ 2.
Hướng dẫn: Chọn đáp án B
Nếu sóng dừng trên dây một đầu cố định một đầu tự do thì các tần số f 1 , 3 f 1 , 5 f 1 , …
Nếu sóng dừng trên dây hai đầu cố định thì các tần số f 1 , 2 f 1 , 3 f 1 , . . .
Như vậy, trong bài toán này thì sợi dây hai đầu cố định nên số nút bằng số bụng cộng 1.
Đúng 0
Bình luận (0)
Chứng minh theo quy nạp
Dãy số Fn=2^2^n +1 với n thuộc N gọi là các số fermat
a) Chứng minh Fn=F0F1.....Fn-1 +2 với mọi n nguyên dương
b) Từ đó chứng minh (Fm,Fn)=1 với mọi m khác n nguyên dương
Cho dãy số : Fo = 1 ; F1 = 1
Fn+2 = F ( n ) + F ( n + 1 )
a ) Tính tổng 10 số hạng đầu tiên của dãy
b ) Tìm F20