Cho đường thẳng d: 2x-3y +3=0 và M (8;2) .Tọa độ của điểm M’ đối xứng với M qua d là:
A.(-4; 8)
B.(-4; -8)
C. (4; 8)
D.tất cả sai
PB
Những câu hỏi liên quan
Đường thẳng d đi qua điểm M(1, 2) và song song với đường thẳng delta: 2x+3y-12=0 có phương trình tổng quát là:
a. 4x+6y+1=0 b.2x+3y-8=0
c. 4x-3y-8=0 c. 2x+3y+8=0
Xem thêm câu trả lời
Cho hai đường thẳng d: 2x- y + 3= 0 và ∆: x+ 3y – 2= 0. Phương trình đường thẳng d’ đối xứng với d qua là:
A. 11x + 13y -2= 0
B.11x -2y = -13
C.13x-11y+3= 0
D.11x-13y+2= 0
Đáp án B
+Giao điểm của d và là nghiệm của hệ
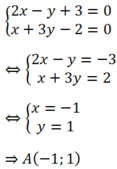
+Lấy M(0; 3) thuộc d. Tìm M’ đối xứng M qua
Viết phương trình đường thẳng đi qua M(0;3) và vuông góc với :
3( x-0) -1( y-3) =0 hay 3x –y+3= 0
+Gọi H là giao điểm của và đường thẳng . Tọa độ H là nghiệm của hệ
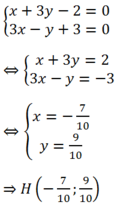
+Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ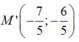 
Viết phương trình đường thẳng d’đi qua 2 điểm A và M’: điểm đi qua A( -1 ;1) , vectơ chỉ phương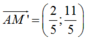 
=> vectơ pháp tuyến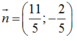 
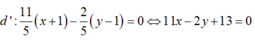
Đúng 0
Bình luận (0)
Trong mặt phẳng
v
→
(
−
2
;
1
)
cho, đường thẳng d có phương trình 2x − 3y + 3 0, đường thẳng
d
1
có phương trình
2
x
−
3
y
−
5
0...
Đọc tiếp
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Viết phương trình của đường thẳng d’ là ảnh của d qua T v → .
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Khi đó M′ = T v → ( M ) = (0 − 2; 1 + 1) = (−2; 2) thuộc d'.
Vì d' song song với d nên phương trình của nó có dạng 2x − 3y + C = 0.
Do M' ∈ d′ nên 2.(−2) − 3.2 + C = 0. Từ đó suy ra C = 10 .
Do đó d' có phương trình 2x − 3y + 10 = 0.
Đúng 0
Bình luận (0)
1. Cho M(3;-1) và đường thẳng d: 3x-4y+120. Tìm N đối xứng với M qua d.2. Cho M(8;2) và đường thẳng d: 2x-3y+30. Tìm N đối xứng với M qua d.3. Cho đường thẳng d: x+y-50 và I(2;0). Tìm điểm M thuộc d sao cho MI3.4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-70 và d2: 5x+3y-290.a.Tìm điểm A và viết pt cạnh BC.b. Viết pt cạnh AC.CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
Đọc tiếp
1. Cho M(3;-1) và đường thẳng d: 3x-4y+12=0. Tìm N đối xứng với M qua d.
2. Cho M(8;2) và đường thẳng d: 2x-3y+3=0. Tìm N đối xứng với M qua d.
3. Cho đường thẳng d: x+y-5=0 và I(2;0). Tìm điểm M thuộc d sao cho MI=3.
4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-7=0 và d2: 5x+3y-29=0.
a.Tìm điểm A và viết pt cạnh BC.
b. Viết pt cạnh AC.
CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
trl ; bạn kia đúng r
-
_
----------------
chọn và giải ra luôn nhé Trong mặt phẳng Oxy, phương trình đường thẳng d đi qua A(1;-2) và vuông góc với đường thẳng ∆:3x-2y+x=0 là A. 3x-2y-7=0 B.2x+3y+4=0 C.x+3y+5=0 D.2x+3y-3=0
cho đường thẳng y = 2mx + 3 - m - x (d). Xác định m để đường thẳng d đi qua giao điểm của hai đường thẳng 2x -3y = 8 và y = -x + 1
https://i.imgur.com/ZgUUfUK.jpg
Câu 3. Cho điểm A(1; 2) và đường thẳng d: 2x - 3y - 1 = 0 Viết phương trình đường thẳng triangle delta*i qua A và song song với d.
Ta có: \(\Delta//d\Rightarrow\Delta:2x-3y+c=0\left(c\ne-1\right)\)
\(A\left(1;2\right)\in\Delta:2\cdot1-3\cdot2+c=0\)
\(\Leftrightarrow c=4\)
Vậy: \(\Delta:2x-3y+4=0\)
Đúng 2
Bình luận (0)
Vì (Δ)//d nên Δ: 2x-3y+c=0
Thay x=1 và y=2 vào Δ, ta được:
c+2-6=0
=>c=4
Đúng 1
Bình luận (0)
Trong mặt phẳng
v
→
(
−
2
;
1
)
cho, đường thẳng d có phương trình 2x − 3y + 3 0, đường thẳng
d
1
có phương trình
2
x
−
3
y
−
5
0
.
Tìm t...
Đọc tiếp
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Tìm tọa độ của w → có giá vuông góc với đường thẳng d để d 1 là ảnh của d qua T w →
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của
d
2
là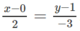 
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
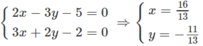
Từ đó suy ra
Đúng 0
Bình luận (0)
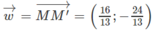
Trg mp tọa độ Oxy, cho 2 đường thẳng d: 2x - 3y + 3 = 0 và d': 2x - 3y - 5 = 0. Tìm tọa độ v có phương vuông góc với d để Tv (d) = d'