Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4;3)
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm phương trình chính tắc của Hyperbol mà hình chữ nhật cơ sở có một đỉnh là (2;-3)
A. 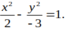
B. 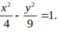
C. 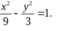
D. 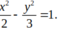
Chọn B.
Gọi (H): x 2 a 2 - y 2 b 2 = 1 .
Tọa độ đỉnh của hình chữ nhật cơ sở là A(a; B); B( a; -b); C( -a; b) và D( –a; -b).
Hình chữ nhật cơ sở của (H) có một đỉnh là (2;-3),
suy ra a = 2 b = 3 .
Phương trình chính tắc của (H) là
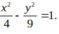
Phương trình x 2 m 2 + y 2 36 = 1 là phương trình chính tắc của elip có hình chữ nhật cơ sở với diện tích bằng 300 thì:
A. m = ± 5 2
B. m = ± 15 2
C. m = ± 25 2
D. Không tồn tại m
Phương trình chính tắc của elip có độ dài trục nhỏ bằng 8, hình chữ nhật cơ sở có chu vi bằng 40 là:
A. x 2 36 + y 2 16 = 1
B. 36 x 2 + 16 y 2 = 1
C. x 2 144 + y 2 64 = 1
D. 36 x 2 + 16 y 2 = 576
Ta có độ dài trục nhỏ bằng 8 nên 2b = 8 b = 4
Hình chữ nhật cơ sở có chu vi bằng 40 nên 4a + 4b = 40
Mà b = 4 nên a= 6
Phương trình chính tắc của (E): x 2 36 + y 2 16 = 1
Đáp án A
Trong mặt phẳng tọa độ Oxy, phương trình chính tắc của (E) nhận điểm M(4;3) là một đỉnh của hình chữ nhật cơ sở là
A. x 2 16 + y 2 9 = 1
B. x 2 16 + y 2 4 = 1
C. x 2 16 + y 2 3 = 1
D. x 2 9 + y 2 4 = 1
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:
A. x 2 25 + y 2 16 = 1.
B. x 2 5 + y 2 4 = 1.
C. x 2 25 + y 2 9 = 1.
D. x 5 + y 4 = 1.
1 .cho hình chóp có đáy là đa giác lồi 2019 đỉnh. tìm số cạnh của hình chóp
2. sô gía trị nguyên của tham số m để phương trình sin^2x+(m-1)cosx+1-m=0 có đúng 4 nghiệm thuộc khoảng [0;5pi/2]
3. tìm phương trình chính tắc của elip có một đỉnh A(4;0) và độ dài trục nhỏ bằng 6
Lập PT chính tắc hypebol biết 1 đỉnh của hình chữ nhật cơ sở là (2; -3)
a) Viết phương trình chính tắc của elip (E) đi qua điểm \(A\left(0;2\right)\) và có một tiêu điểm là \(F_1\left(-\sqrt{5};0\right)\)
b) Tìm độ dài trục lớn, trục nhỉ, tiêu cự và tỉ số \(\dfrac{c}{a}\) của elip (E)
c) Tìm diện tích của hình chữ nhât cơ sở của (E)
a, Phương trình chính tắc của (E) có dạng
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) với 0<b<a
Ta có A(0;2) \(\in\left(E\right)\)<=>b=2
(E) có tiêu điểm F1\(\left(-\sqrt{5};0\right)\) => c=\(\sqrt{5}\)
Ta có \(a^2=b^2+c^2=4+5=9\)=>a=3
==> (E) \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
b, 2a = 6; 2b = 4; 2c = \(2\sqrt{5}\)=>\(\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}\)
c, S=4ab=24
Lập phương trình chính tắc của Elip, biết:
Elip có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông có diệc tích bằng 32.
Do 2 đỉnh trên trục nhỏ và 2 tiêu điểm tạo thành hình vuông \(\Rightarrow b=c\)
Mặt khác diện tích hình vuông bằng 32 \(\Rightarrow\dfrac{1}{2}.2b.2c=32\Rightarrow b^2=16\)
\(\Rightarrow a^2=b^2+c^2=2b^2=32\)
Phương trình: \(\dfrac{x^2}{32}+\dfrac{y^2}{16}=1\)