Cho hai số thực a và b thoả mãn lim x → + ∞ 4 x 2 - 3 x + 1 2 x + 1 - a x - b = 0 . Khi đó a+2b bằng:
PB
Những câu hỏi liên quan
tìm các số thực a,b thoả mãn \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2-ax+1}-bx\right)=2\)
Giới hạn đã cho hữu hạn khi và chỉ khi \(b=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2-ax+1}-x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{-ax+1}{\sqrt{x^2-ax+1}+x}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-a+\dfrac{1}{x}}{\sqrt{1-\dfrac{a}{x}+\dfrac{1}{x^2}}+1}=-\dfrac{a}{2}\)
\(\Rightarrow-\dfrac{a}{2}=2\Rightarrow a=-4\)
Vậy \(\left(a;b\right)=\left(-4;1\right)\)
Đúng 3
Bình luận (0)
tìm các số thực a,b thoả mãn \(\lim\limits_{x\rightarrow1}\left(\dfrac{x^2+ax+b}{x^2-1}\right)=-\dfrac{1}{2}\)
TT
17 tháng 3 2023 lúc 21:46
Tìm các số thực a, b thoả mãn:
\(\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left[\left(a^3+b^3\right)x^2-\left(x+a^2b\right)\sqrt{x^2+2\left(ab\right)^2}\right]}{x-b-1}\)
H24
Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 12:55
Cho hai hàm số và y gleft( x right) frac{x}{{x + 1}}.a) Giả sử left( {{x_n}} right) là dãy số bất kì thoả mãn {x_n} ne - 1 với mọi n và {x_n} to 1 khi n to + infty . Tìm giới hạn lim left[ {fleft( {{x_n}} right) + gleft( {{x_n}} right)} right].b) Từ đó, tìm giới hạn mathop {lim }limits_{x to 1} left[ {fleft( x right) + gleft( x right)} right], và so sánh với mathop {lim }limits_{x to 1} {rm{ }}fleft( x right) + mathop {lim }limits_{x to 1} gleft( x right).
Đọc tiếp
Cho hai hàm số và \(y = g\left( x \right) = \frac{x}{{x + 1}}\).
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thoả mãn \({x_n} \ne - 1\) với mọi \(n\) và \({x_n} \to 1\) khi \(n \to + \infty \). Tìm giới hạn \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right]\).
b) Từ đó, tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\), và so sánh với \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\).
a) \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \lim \left( {2{x_n} + \frac{{{x_n}}}{{{x_n} + 1}}} \right) = 2\lim {x_n} + \lim \frac{{{x_n}}}{{{x_n} + 1}} = 2.1 + \frac{1}{{1 + 1}} = \frac{5}{2}\)
b) Vì \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \frac{5}{2}\) nên \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \frac{5}{2}\) (1).
Ta có: \(\lim {\rm{ }}f\left( {{x_n}} \right) = \lim 2{x_n} = 2\lim {x_n} = 2.1 = 2 \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) = 2\)
\(\lim g\left( {{x_n}} \right) = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \frac{1}{{1 + 1}} = \frac{1}{2} \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}g\left( x \right) = \frac{1}{2}\)
Vậy \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 2 + \frac{1}{2} = \frac{5}{2}\) (2).
Từ (1) và (2) suy ra \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\)
Đúng 0
Bình luận (0)
Cho hai số thực dương a,b thoả mãn a+b 2018 và
∫
a
b
x
x
+
2018
-
x
d
x
10
Tích phân
∫
a
b
sin
πx
3...
Đọc tiếp
Cho hai số thực dương a,b thoả mãn a+b = 2018 và ∫ a b x x + 2018 - x d x = 10 Tích phân ∫ a b sin πx 3 d x bằng
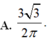
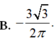
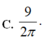
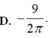
Cho hai số thực dương a,b thoả mãn a + b 2018 và
∫
a
b
x
x
+
2018
-
x
d
x
10
Tích phân
∫
a
b
sin
π
x
3...
Đọc tiếp
Cho hai số thực dương a,b thoả mãn a + b = 2018 và ∫ a b x x + 2018 - x d x = 10 Tích phân ∫ a b sin π x 3 d x bằng
A. 3 3 2 π
B. - 3 3 2 π
C. 9 2 π
D. - 9 2 π
Cho hai số thực dương a,b thoả mãn a+b2018 và
∫
a
b
x
x
+
2018
-
x
d
x
10
. Tích phân
∫
a
b
s
i
n
(
π
x...
Đọc tiếp
Cho hai số thực dương a,b thoả mãn a+b=2018 và ∫ a b x x + 2018 - x d x = 10 . Tích phân ∫ a b s i n ( π x 3 ) d x bằng
A. 3 3 2 π
B. - 3 3 2 π
C. 9 2 π
D. - 9 2 π
Cho hai số thực a,b thoả mãn a+b-ab= -1 và a^2+b^2=13. Tính P= | a^3-b^3 |
\(a^2+b^2=13\Leftrightarrow a^2+b^2+2ab-2ab=13\Leftrightarrow\left(a+b\right)^2-2ab=13\)
Mà \(a+b-ab=-1\Leftrightarrow ab=a+b+1\)Thay vào phương trình trêm ta có:
\(\left(a+b\right)^2-2\left(a+b+1\right)=13\)
<=> \(\left(a+b\right)^2-2\left(a+b\right)+1=16\)
<=> \(\left(a+b+1\right)^2=4^2\)
<=> \(a+b+1=\pm4\)=> \(ab=\pm4\)
Ta lại có: \(a^2+b^2=13\Leftrightarrow\left(a-b\right)^2+2ab=13\)
+) Với ab=4
thay vào ta có: \(\left(a-b\right)^2+8=13\Leftrightarrow\left(a-b\right)^2=5\Leftrightarrow\left|a-b\right|=\sqrt{5}\)
=> \(P=\left|a^3-b^3\right|=\left|\left(a-b\right)\left(a^2+b^2+ab\right)\right|=\left|a-b\right|\left|a^2+b^2+ab\right|\)
\(=\sqrt{5}\left(13+4\right)=17\sqrt{5}\)
+) Với ab=-4 . Em làm tương tự nhé!
Đúng 0
Bình luận (0)
Cho hai số thực x, y thoả mãn phương trình
x
+
2
i
3
+
4
y
i
. Khi đó giá trị của x và y là: A.
x
3
,
y
−
1
2
B. x 3, y 2 C.
x
3
i
,
y
1
2
D.
x
3...
Đọc tiếp
Cho hai số thực x, y thoả mãn phương trình x + 2 i = 3 + 4 y i . Khi đó giá trị của x và y là:
A. x = 3 , y = − 1 2
B. x = 3, y = 2
C. x = 3 i , y = 1 2
D. x = 3 , y = 1 2
