Phương trình 3 . tan x + 1 . ( sin 2 x + 1 ) = 0 có nghiệm là
![]()
![]()
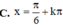
![]()
Phương trình tanx + tan(x + π 3 ) + tan(x + 2 π 3 ) = 3 3 tương đương với phương trình.
A. cot x = 3
B. cot 3x = 3
C. tan x = 3
D. tan 3x = 3
Giải phương trình 3 . tan x - 3 = 0
![]()
![]()
![]()
![]()
Phương trình 3 . tan x - 3 = 0 có nghiệm là:
![]()
![]()
![]()
![]()
Phương trình tan x = 3 có tập nghiệm là:
A. π 3 + k 2 π , k ∈ ℤ
B. π 6 + k π , k ∈ ℤ
C. ∅
D. π 3 + k π , k ∈ ℤ
Phương trình tan ( x + π/ 3) có nghiệm là:
![]()
![]()
![]()
![]()
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
Đặt \(tan\left(x+\dfrac{\pi}{3}\right)=t\)
\(\Rightarrow t^2+\left(\sqrt{3}-1\right)t-\sqrt{3}=0\)
\(\Leftrightarrow t\left(t-1\right)+\sqrt{3}\left(t-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tan\left(x+\dfrac{\pi}{3}\right)=1\\tan\left(x+\dfrac{\pi}{3}\right)=-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=-\dfrac{2\pi}{3}+k\pi\end{matrix}\right.\)
Tất cả các nghiệm của phương trình tan x + 3 . c o t x - 3 - 1 = 0 là

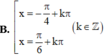
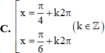
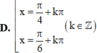
giải phương trình: \(\tan\left(\dfrac{3}{2}-x\right)+\dfrac{\sin x}{1+\cos x}=2\)
phương trình tan^x+cot^x-3(tanx+cotx)-2=0 có bao nhiêu nghiệm thuộc(0,pi)