Cho hàm số f ( x ) = m x - 1 3 x 3 . Với giá trị nào của m thì x = -1 là nghiệm của bất phương trình f'(x) < 2 ?
A. m > 3
B. m < 3
C. m = 3
D. m < 1
PB
Những câu hỏi liên quan
Cho hàm số
f
(
x
)
m
x
−
1
3
x
3
. Với giá trị nào của m thì x -1 là nghiệm của bất phương trình
f
(
x
)
2
? A. m3 B. m 3 C.m 3 D. m1
Đọc tiếp
Cho hàm số f ( x ) = m x − 1 3 x 3 . Với giá trị nào của m thì x= -1 là nghiệm của bất phương trình f ' ( x ) < 2 ?
A. m>3
B. m< 3
C.m = 3
D. m<1
Ta có f ' x = m − x 2 .
Để x= - 1 là nghiệm của bất phương trình
f ' ( x ) < 2
⇒ f ' 1 < 2 ⇔ m − 1 < 2 ⇔ m < 3.
Chọn đáp án B
Đúng 0
Bình luận (0)
Cho hàm số f(x) a
x
2
+ bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực mm thì phương trình f(|x|) – 1 m có đúng 3 nghiệm phân biệt. A. m 3. B. m 3. C. m 2. D. −2 m 2.
Đọc tiếp
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực mm thì phương trình f(|x|) – 1 = m có đúng 3 nghiệm phân biệt.
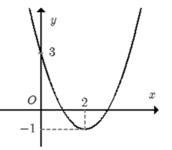
A. m = 3.
B. m > 3.
C. m = 2.
D. −2 < m < 2.
cho hàm số f(x)=sin2x+2(1-2m)cos2x-2mx+1. Với giá trị nào của tham số m thì phương trình f'(x)=0 có nghiệm
\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)
Phương trình \(f'\left(x\right)=0\) có nghiệm
\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm
\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(1^2+4\left(1-2m\right)^2\ge m^2\)
\(\Leftrightarrow15m^2-16m+5\ge0\)
\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)
Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m
Đúng 0
Bình luận (0)
Cho hai hàm số y = (m - 1)x + 3 và y = (3 - m)x + 1, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhaub, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau
a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
Đúng 0
Bình luận (0)
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) có bảng biến thiên như sau:
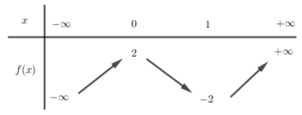
Với giá trị nào của tham số m thì phương trình |f(x) − 1| = m có bốn nghiệm phân biệt.
A. m = 1.
B. 1 < m < 3.
C. 0 < m < 1.
D. m ≥ 3.
Cho hàm số y f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng? A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số. B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y f(x).
C. Số M f(
x
0
) trong đó
x
0
∈ D là giá trị lớn nhất của hàm số y f(x) nếu M f(x), ∀x ∈ D D. Nếu tồn tại
x
0
∈ D...
Đọc tiếp
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
Đúng 0
Bình luận (0)
Câu1 :Với giá trị nào của m thì hàm số bậc nhất y ( m – 1)x + 3 là hàm số đồng biến A.m 1 B. m 1 C. m 1 D. m -1Câu2 :Với giá trị nào của m thì hàm số bậc nhất y ( m – 1)x + 3 là hàm số nghịch biếnA. m 1 B. m 1 C. m 1 D. m -1Câu3 :Với giá trị nào của m thì đồ thị các hàm số y 2x + (3+m) và y 3x + 5 cắt nhau tại một điểm trên trục tung?A. m 5 B. m 3 ...
Đọc tiếp
Câu1 :Với giá trị nào của m thì hàm số bậc nhất y = ( m – 1)x + 3 là hàm số đồng biến
A.m =1 B. m > 1 C. m < 1 D. m < -1
Câu2 :Với giá trị nào của m thì hàm số bậc nhất y = ( m – 1)x + 3 là hàm số nghịch biến
A. m =1 B. m > 1 C. m < 1 D. m < -1
Câu3 :Với giá trị nào của m thì đồ thị các hàm số y = 2x + (3+m) và y = 3x + 5 cắt nhau tại một điểm trên trục tung?
A. m = 5 B. m = 3 C. m = 2 D. m = 8
Câu4 :Cho hai hàm số y = (m -2) x + 1 và y = 4x + 5. Với giá trị nào của m thì hai đường thẳng
a)Cắt nhau
A. m > 2 B. m 6 C. m < 5 D. m 4
b) Song song nhau
A.m = 2 B. m = 6 C. m = 5 D.m = 4
Câu5 :Điểm A(2;-1) thuộc đồ thị hàm số nào?
A. y=2x-3 B. y=-x C. y= D. y= .
Câu6 :Điểm nào sau đây thuộc đồ thị hàm số y= ?
A. ( B. (2; 2) C. (0;2) D. (2;0)
Câu7 :Xác định hệ số a của hàm số y = m x +3
A. a =1 B.a=m C.a=0 D.a=3
Câu8 : Biết hàm số nào là hàm số bậc nhất
A. y = x B. y = x2 C. y = 0x+3 D. y = 2 + 2x2
Câu 9 : Đường thẳng y = x -2 đi qua đi nào sau đây?
A. (0; -2) B.(0;1) C.(1; -2) D.(0;2)
Câu10 : Đường thẳng nào sau đây song song với đường thẳng y = 2x - 3
A. y= 2x -3 B. y= 2x +3 C.y= 3x-2 D.y=3x +2
Câu11: Đường thẳng nào sau đây cắt đường thẳng y = 4x -1
A. y= 4x B.y= 3x-1 C.y= 4x- 1 D. y=4x+1
Câu12: Hệ số góc của đường thẳng y=2x+1 là
A. 0 B. 1 C. 1/2 D. 2
Câu13:Cho hàm số bậc nhất y= ax + 2 có đồ thị hàm số đi qua điểm A(4,1). Hệ số góc của đường thẳng là
A. 2 B. 4 C. -1/4 D. ¼
Câu14:Đường thẳng y = -2x + 3 có tung độ góc là
A. 2 B. -2 C. 1 D. 3
Câu15: Cho hai đường thẳng y = 3x + m và y= 3x +1 tìm m để hai đường thẳng song trùng nhau
A. m= 2 B. m= 3 C.m=1 D.m=-2
H24
4 tháng 4 2021 lúc 17:21
1. Cho hàm số yx^3-3mx^2+3left(2m-1right)x+1 . Với giá trị nào của m thì fleft(xright)-6x0 với mọi x2A. m 1/2 B. m -1/2 C. m 1 D. m ≤ 02. Cho hai hàm số f(x) và g(x) đều có đạo hàm trên R và thỏa mãn : f^3left(2-xright)-2f^2left(2+3xright)+x^2gleft(xright)+36x0 với mọi x thuộc R.Tính A3fleft(2right)+4fleft(2right)3. Biết hàm số f(x) - f(2x) có đạo hàm bằng 18 tại x1 và đạo hàm bằng 2000 tại x2. Tính đạo hàm của hàm số f(x) - f(4x) tại x1
Đọc tiếp
1. Cho hàm số \(y=x^3-3mx^2+3\left(2m-1\right)x+1\) . Với giá trị nào của m thì \(f'\left(x\right)-6x>0\) với mọi x>2
A. m > 1/2 B. m < -1/2 C. m >1 D. m ≤ 0
2. Cho hai hàm số f(x) và g(x) đều có đạo hàm trên R và thỏa mãn :
\(f^3\left(2-x\right)-2f^2\left(2+3x\right)+x^2g\left(x\right)+36x=0\) với mọi x thuộc R.
Tính \(A=3f\left(2\right)+4f'\left(2\right)\)
3. Biết hàm số f(x) - f(2x) có đạo hàm bằng 18 tại x=1 và đạo hàm bằng 2000 tại x=2. Tính đạo hàm của hàm số f(x) - f(4x) tại x=1
1.
\(f'\left(x\right)=3x^2-6mx+3\left(2m-1\right)\)
\(f'\left(x\right)-6x=3x^2-3.2\left(m+1\right)x+3\left(2m-1\right)>0\)
\(\Leftrightarrow x^2-2\left(m+1\right)x+2m-1>0\)
\(\Leftrightarrow x^2-2x-1>2m\left(x-1\right)\)
Do \(x>2\Rightarrow x-1>0\) nên BPT tương đương:
\(\dfrac{x^2-2x-1}{x-1}>2m\Leftrightarrow\dfrac{\left(x-1\right)^2-2}{x-1}>2m\)
Đặt \(t=x-1>1\Rightarrow\dfrac{t^2-2}{t}>2m\Leftrightarrow f\left(t\right)=t-\dfrac{2}{t}>2m\)
Xét hàm \(f\left(t\right)\) với \(t>1\) : \(f'\left(t\right)=1+\dfrac{2}{t^2}>0\) ; \(\forall t\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t\right)>f\left(1\right)=-1\Rightarrow\) BPT đúng với mọi \(t>1\) khi \(2m< -1\Rightarrow m< -\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
2.
Thay \(x=0\) vào giả thiết:
\(f^3\left(2\right)-2f^2\left(2\right)=0\Leftrightarrow f^2\left(2\right)\left[f\left(2\right)-2\right]=0\Rightarrow\left[{}\begin{matrix}f\left(2\right)=0\\f\left(2\right)=2\end{matrix}\right.\)
Đạo hàm 2 vế giả thiết:
\(-3f^2\left(2-x\right).f'\left(2-x\right)-12f\left(2+3x\right).f'\left(2+3x\right)+2x.g\left(x\right)+x^2.g'\left(x\right)+36=0\) (1)
Thế \(x=0\) vào (1) ta được:
\(-3f^2\left(2\right).f'\left(2\right)-12f\left(2\right).f'\left(2\right)+36=0\)
\(\Leftrightarrow f^2\left(2\right).f'\left(2\right)+4f\left(2\right).f'\left(2\right)-12=0\) (2)
Với \(f\left(2\right)=0\) thế vào (2) \(\Rightarrow-12=0\) ko thỏa mãn (loại)
\(\Rightarrow f\left(2\right)=2\)
Thế vào (2):
\(4f'\left(2\right)+8f'\left(2\right)-12=0\Leftrightarrow f'\left(2\right)=1\)
\(\Rightarrow A=3.2+4.1\)
Đúng 1
Bình luận (0)
3.
Đặt \(g\left(x\right)=f\left(x\right)-f\left(2x\right)\)
\(\Rightarrow g'\left(x\right)=f'\left(x\right)-2f'\left(2x\right)\)
Thay \(x=1\Rightarrow18=f'\left(1\right)-2f'\left(2\right)\) (1)
Thay \(x=2\Rightarrow2000=f'\left(2\right)-2f'\left(4\right)\Rightarrow4000=2f'\left(2\right)-4f'\left(4\right)\) (2)
Cộng vế (1) và (2):
\(f'\left(1\right)-4f'\left(4\right)=4018\)
Đặt \(h\left(x\right)=f\left(x\right)-f\left(4x\right)\Rightarrow h'\left(x\right)=f'\left(x\right)-4f'\left(4x\right)\)
Thay \(x=1\Rightarrow h'\left(1\right)=f'\left(1\right)-4f'\left(4\right)=4018\)
Đúng 1
Bình luận (0)
Cho hàm số y f(x) có đồ thị như hình dưới đây. Tìm tất cả các giá trị thực của tham số m để bất phương trình
2
f
x
+
x
2
4
x
+
m
nghiệm đúng với mọi
x
∈
-
1
;
3...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình dưới đây.
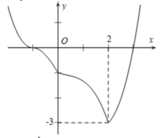
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 f x + x 2 > 4 x + m nghiệm đúng với mọi x ∈ - 1 ; 3 .
