Tất cả các nghiệm phức của phương trình z 2 + 5 = 0 là
A. ± 5
B. ± 5 i
C. ± 5 i
D. ± 5
Tất cả các nghiệm phức của phương trình z 2 + 5 = 0 là
A. ± 5
B. ± 5 i
C. ± 5 i
D. ± 5
Có x 2 + 5 = 0 ⇔ z 2 = 5 i 2 ⇔ z = ± 5 i
Chọn đáp án C.
Tất cả các nghiệm phức của phương trình z 2 + 5 = 0 là
![]()
![]()
![]()
![]()
Tất cả các nghiệm phức của phương trình z 3 − 64 z 2 + 2 = 0 có tổng môđun là
A. 4 + 2 2
B. 4 + 2
C. 8 + 2
D. 12 + 2 2
Tất cả các nghiệm phức của phương trình z 3 - 64 z 2 + 2 = 0 có tổng môđun là
A. 4+2 2 .
B. 4 + 2 .
C. 8 + 2 .
D. 12+2 2
Xác định tất cả các số thực m để phương trình
z 2 - 2 z + 1 - m = 0 có nghiệm phức z thỏa mãn z = 2 .
A. m = 1 ; m = 9 .
B. m = - 3
C. m = - 3 ; m = 1 ; m = 9 .
D. m = - 3 ; m = 9
Tất cả các nghiệm phức của phương trình ( z 3 − 64 ) ( z 2 + 2 ) = 0 có tổng môđun là
A. 4 + 2 2
B. 4 + 2
C. 8 + 2
D. 12 + 2 2
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
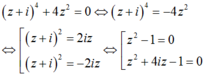
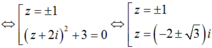
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Biết z 1 , z 2 là 2 nghiệm phức của phương trình: 2 z 2 - ( 3 - 1 ) z + 5 = 0 . Chọn khẳng định đúng
A . z 1 . z 2 = 1
B . z 1 = z 2 ¯
C . z 1 2 = z 2 2
D . z 1 = - z 2
Cho phương trình ( m - 5 ) . 3 x + ( 2 m - 2 ) . 2 x . 3 x + ( 1 - m ) . 4 x = 0 , tập hợp tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt là khoảng (a;b). Tính S=a+b
A.4
B.5
C.6
D.8