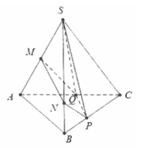
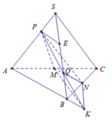
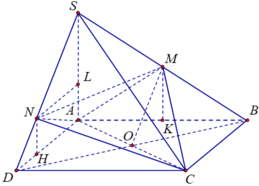
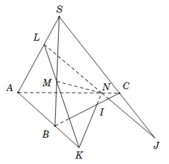
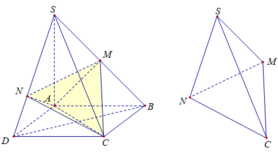
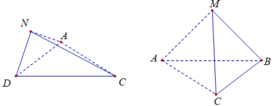
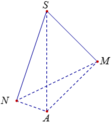
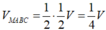Cho tứ diện SABC và hai điểm M, N lần lượt thuộc các cạnh SA, SB sao cho
S
M
A
M
=
1
2
,
S
N
B
N
=
2
. Mặt phăng (P) đi qua hai điểm M, N và song song với cạnh SC, cắt AC, BC lần lượt tại L, K. Tính tỉ số thể tích
V
S
C
M
N
K
L
V
S
A
B
C
A. V S C M N K L V S A B C = 4 9
B. V S C M N K L V S A B C = 1 3
C. V S C M N K L V S A B C = 2 3
D. V S C M N K L V S A B C = 1 4