Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm A1,A2
sao cho AA1=A1A2=A2S.
. Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua A1,A2.
. Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại B1,C1.
. Mặt phẳng (Q) cắt các canhj SB, SC lần lượt tại B2,C2.
. Chứng minh BB1=B1B2=B2Svà CC1=C1C2=C2S.
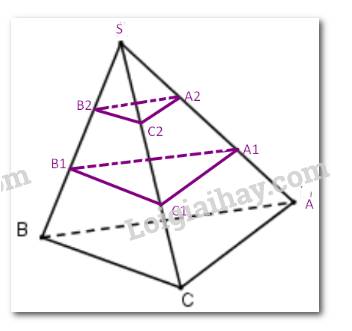
Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SC ta có:
\(\frac{{{C_2}S}}{{{A_2}S}} = \frac{{{C_1}{C_2}}}{{{A_1}{A_{2\;}}}} = \frac{{C{C_1}}}{{A{A_1}}}\) mà \(A{A_1} = {A_1}{A_2} = {A_2}S\).
Suy ra \(C{C_1} = {C_1}{C_2} = {C_2}S\).
Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SB ta có:
\(\frac{{{B_2}S}}{{{A_2}S}} = \frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = \frac{{B{B_1}}}{{A{A_1}}}\) mà \(A{A_1} = A{A_2} = {A_2}S\).
Suy ra \(B{B_1} = {B_1}{B_2} = {B_2}S\).