Tính tổng T tất cả các nghiệm của phương trình log 5 25 - 5 x + x - 3 = 0 .
A.1
B.3
C.25
D.2
31. Tổng tất cả các nghiệm của phương trình log(8.5x + 20x ) = x + log 25 bằng ?
Lời giải:
$\log(8.5^x+20^x)=x+\log 25$
$\Rightarrow 8.5^x+20^x=10^{x+\log 25}=10^x.25$
$\Rightarrow \frac{8.5^x+20^x}{10^x}=25$
$\Leftrightarrow \frac{8}{2^x}+2^x=25$
Đặt $2^x=t$ thì $\frac{8}{t}+t=25$
$\Leftrightarrow t^2-25t+8=0$
Dễ thấy PT trên luôn có 2 nghiệm dương $t_1,t_2$ nên kéo theo PT ban đầu có 2 nghiệm $x_1,x_2$
Tổng các nghiệm $x_1+x_2=\log_2(t_1)+\log_2(t_2)=\log_2(t_1t_2)=\log_2(8)=3$
Tìm tất cả các nghiệm của phương trình log x + log ( x - 9 ) = 1
A. {10}
B. {9}
C. {1;9}
D. {-1;10}
Tổng tất cả các nghiệm của phương trình log5(6-5x)=1-x bằng
ĐKXĐ: \(6-5^x>0\Rightarrow5^x< 6\)
\(log_5\left(6-5^x\right)=1-x\Leftrightarrow6-5^x=5^{1-x}\)
\(\Leftrightarrow5^x-6+\frac{5}{5^x}=0\Leftrightarrow\left(5^x\right)^2-6.5^x+5=0\)
\(\Rightarrow\left[{}\begin{matrix}5^x=1\\5^x=5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\) \(\Rightarrow\sum x=0+1=1\)
Tính tổng T tất cả các nghiệm của phương trình
( x - 3 ) 2 x 2 - 5 x = 1 .
A. T = 0
B. T = 4
C. T = 13 2
D. T = 15 2
Ta xét các trường hợp sau:
+ TH1. x- 3= 1 hay x= 4. Khi đó; phương trình đã cho trở thành : 112= 1 luôn đúng.
=> x= 4 là nghiệm của phương trình.
+ TH2. .
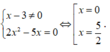
Vậy phương trình đã cho có ba nghiệm
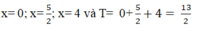
Chọn C.
Tính tổng tất cả các nghiệm của phương trình sau 3 2 x + 8 - 4 . 3 x + 5 + 27 = 0
A. -5
B. 5
C. 4 27
D. - 4 27
Tính tổng tất cả các nghiệm của phương trình sau 3 2 x + 8 - 4 . 3 x + 5 + 27 = 0
A. -5
B. 5
C. 4 27
D. - 4 27
Tính tổng tất cả các nghiệm của phương trình sau 3 2 x + 8 − 4.3 x + 5 + 27 = 0.
A. -5
B. 5
C. 4 27
D. − 4 27
Đáp án A
P T ⇔ 3 x + 5 2 9 − 4.3 x + 5 + 27 = 0 ⇔ 3 x + 5 = 27 3 x + 5 = 9 ⇔ x = − 2 x = − 3 ⇒ x 1 + x 2 = − 5.
Tính tổng tất cả các nghiệm của phương trình sau 3 2 x + 8 − 4.3 x + 5 + 27 = 0
A. - 5
B. 5
C. 4 27
D. - 4 27
Đáp án A
3 2 x + 8 − 4.3 x + 5 + 27 = 0 ⇔ 3 2 x + 4 − 12.3 x + 4 − 27 = 0 ⇔ 3 x + 4 = 3 3 x + 4 = 9 ⇔ x = − 3 x = − 2
Vậy tổng các nghiệm của phương trình trên là − 3 + − 2 = − 5
Gọi S là tập hợp tất cả các giá trị của tham số m ∈ Z và phương trình:
logmx-5.x2 - 6x + 12= log\(\sqrt{mx-5}\) \(\sqrt{x+2}\) có nghiệm duy nhất. Tính số phần tử của S
ĐKXĐ: \(mx-5>0\) ; \(x>-2\)
\(log_{mx-5}\left(x^2-6x+12\right)=log_{mx-5}\left(x+2\right)\)
\(\Rightarrow x^2-6x+12=x+2\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
TH1: \(x=2\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5>0\\m.5-5< 0\end{matrix}\right.\) \(\Rightarrow\) ktm
TH2: \(x=5\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5< 0\\m.5-5>0\end{matrix}\right.\)
\(\Rightarrow1< m< \dfrac{5}{2}\Rightarrow m=2\)