Tìm m để giá trị lớn nhất của hàm số y = x 3 - 3 x + 2 m - 1 trên đoạn 0 ; 2 là nhỏ nhất. Giá trị của m thuộc khoảng?
A. 0 ; 1
B. - 1 ; 0
C. 2 3 ; 2
D. - 3 2 ; - 1
cho hàm số y=x^2-3(m+1)x+m^2+3m-2, m là tham số . Tìm tất cả giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
Cho hàm số y= 2x^2 -3(m+1)x +m^2 +3m -2 , m là tham số . TÌm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
Cho hàm số y=(3m-4)x\(^2\) với m\(\ne\)\(\dfrac{4}{3}\). Tìm các giá trị của tham số m để hàm số :
a) Đạt giá trị lớn nhất là 0
b) Đạt giá trị nhỏ nhất là 0
a) Để m đạt giá trị lớn nhất là 0 thì \(y=\left(3m-4\right)x^2\le0\) ⇔ \(3m-4\le0\)
⇔ \(m\le\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị lớn nhất là 0 thì \(m< \dfrac{4}{3}\)
b) Để m đạt giá trị nhỏ nhất là 0 thì \(y=\left(3m-4\right)x^2\ge0\) ⇔ \(3m-4\ge0\)
⇔ \(m\ge\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị nhỏ nhất là 0 thì \(m>\dfrac{4}{3}\)
Câu 1: Cho hàm số y = (3m + 5) x\(^2\) với m \(\ne\) \(\dfrac{-5}{3}\). Tìm các giá trị của tham số m để hàm số:
a) Nghịch biến với mọi x > 0
b) Đồng biến với mọi x >0
c) Đạt giá trị lớn nhất là 0
d) Đạt giá trị nhỏ nhất là 0
Câu 2: Cho hàm số y = \(\left(\sqrt{3k+4}-3\right)x^2\) với k \(\ge\dfrac{-4}{3}\); k \(\ne\dfrac{5}{3}\)
Tính các giá trị của tham số K để hàm số:
a) Nghịch biến với mọi x >0
b) Đồng biến với mọi x >0
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)
Cho hàm số y = 1 3 x 3 - m x 2 + ( 4 m - 3 ) x + 2017 . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên .
A. m = 2
B. m = 3
C. m = 4
D. m = 1
Chọn B
Phương pháp:
Tính y', để hàm số đồng biến trên
ℝ
thì ![]() (y' = 0 tại hữu hạn điểm)
(y' = 0 tại hữu hạn điểm)
Sử dụng ![]()
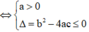
Cách giải:
Tập xác định D = ℝ
Đạo hàm ![]()
Để hàm số đồng biến trên
ℝ
thì ![]() (y' = 0 tại hữu hạn điểm)
(y' = 0 tại hữu hạn điểm)
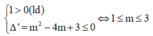
Suy ra giá trị lớn nhất của tham số m thỏa mãn ycbt là m = 3
Cho hàm số y = 1 3 x 3 - m x 2 + ( 4 m - 3 ) x + 2017 . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên R
A.m=2
B.m=3
C.m=4
D.m=1
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
cho hàm số bậc nhất y=(m+3) x+7
a) Tìm giá trị của m để y là hàm số đồng biến
b) Tìm các giá trị của m để y là hàm số nghịch biến
giải chi tiết giúp mk vớiiiiii ạ
a. Hàm đồng biến khi:
\(m+3>0\Rightarrow m>-3\)
b. Hàm nghịch biến khi:
\(m+3< 0\Rightarrow m< -3\)
a) Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\) có bao nhiêu giá trị nguyên của tham số \(a\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
b) Tìm tất cả các giá trị của tham số m để hệ bất pt \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\) có nghiệm
c) Gọi (x;y) là nghiệm của hệ bất pt \(\left\{{}\begin{matrix}x-2y-2\le0\\4x-3y+12\ge0\\x+3y+3\ge0\\2x+y-4\le0\end{matrix}\right.\). Tìm giá trị lớn nhất của biểu thức F=4x+5y-6
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f ( x ) = − x 2 − 4 x + 3 trên đoạn [0;4]
A. M = 4; m = 0
B. M = 29; m = 0
C. M = 3; m = -29
D. M = 4; m = 3