Gọi S là tập hợp tất cả các giá trị của tham số m ∈ ℤ và phương trình log m x - 5 x 2 - 6 x + 12 = log m x - 5 x + 2 có nghiệm duy nhất. Tìm số phân tử của S .
A. 2
B. 3
C. 0
D. 1
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
A. 4.
B. 3.
C. 1.
D. 2.
Gọi S là tập hợp tất cả các giá trị của tham số m ∈ Z và phương trình:
logmx-5.x2 - 6x + 12= log\(\sqrt{mx-5}\) \(\sqrt{x+2}\) có nghiệm duy nhất. Tính số phần tử của S
ĐKXĐ: \(mx-5>0\) ; \(x>-2\)
\(log_{mx-5}\left(x^2-6x+12\right)=log_{mx-5}\left(x+2\right)\)
\(\Rightarrow x^2-6x+12=x+2\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
TH1: \(x=2\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5>0\\m.5-5< 0\end{matrix}\right.\) \(\Rightarrow\) ktm
TH2: \(x=5\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5< 0\\m.5-5>0\end{matrix}\right.\)
\(\Rightarrow1< m< \dfrac{5}{2}\Rightarrow m=2\)
Gọi S là tập hợp tất cả các giá trị của m sao cho 10 m ∈ ℤ và phương trình 2 log m x - 5 2 x 2 - 5 x + 4 = log m x - 5 x 2 + 2 x - 6 có nghiệm duy nhất. Tìm số phần tử của S.
A. 15.
B. 14.
C. 13.
D. 16.
Đáp án A.
Phương trình đã cho tương đương với
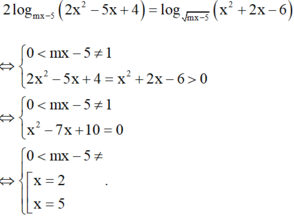
Để phương trình có nghiệm duy nhất
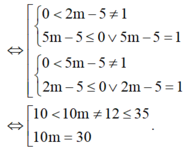
Do 10 m ∈ ℤ nên có 15 giá trị m thỏa mãn yêu cầu bài toán.
Gọi S là tập hợp tất cả các giá trị của m sao cho 10 m ∈ ℤ và phương trình 2 log m x − 5 2 x 2 − 5 x + 4 = log m x − 5 x 2 + 2 x − 6 có nghiệm duy nhất. Tìm số phần tử của S
A. 15
B. 14
C. 13
D. 16
Đáp án A.
Phương trình đã cho tương đương với
2 log m x − 5 2 x 2 − 5 x + 4 = log m x − 5 x 2 + 2 x − 6
⇔ 0 < m x − 5 ≠ 1 2 x 2 − 5 x + 4 = x 2 + 2 x − 6 > 0 ⇔ 0 < m x − 5 ≠ 1 x 2 − 7 x + 10 = 0 ⇔ 0 < m x − 5 ≠ 1 x = 2 x = 5 .
Để phương trình có nghiệm duy nhất
⇔ 0 < 2 m − 5 ≠ 1 5 m − 5 ≤ 0 ∨ 5 m − 5 = 1 0 < 5 m − 5 ≠ 1 2 m − 5 ≤ 0 ∨ 2 m − 5 = 1 ⇔ 10 < 10 m ≠ 12 ≤ 35 10 m = 30 .
Do 10 m ∈ ℤ nên có 15 giá trị m thỏa mãn yêu cầu bài toán
Cho phương trình (m+1)sinx + mcosx = 2m-1 với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình có nghiệm. Tính tổng tất cả các phần tử của S.
![]()
![]()
![]()
![]()
Cho phương trình (m+1)sinx+m cosx=2m-1 với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình có nghiệm. Tính tổng tất cả các phần tử của S.
A.-2.
B. 6.
C.2.
D. -6
Gọi S là tập hợp các giá trị thực của tham số m sao cho phương trình ( x + 1 ) 3 + 3 - m = 3 3 x + m 3 có đúng nghiệm thực. Tích tất cả các phần tử của tập hợp S là
A. -1
B. 1
C. 3
D. 5
Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình m2(x4 - 1) + m(x2 - 1) - 6(x - 1) ≥ 0 đúng với mọi x ∈ R. Tổng giá trị của tất cả các phần tử thuộc S bằng bao nhiêu ?
Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$