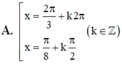
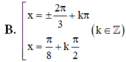
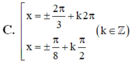
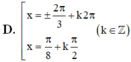
Chọn D

Ta sẽ biến đổi phương trình thành dạng tích

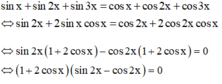
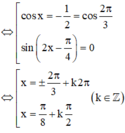
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm

Chọn D

Phương trình tương với:

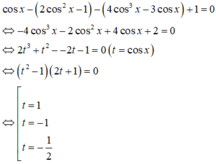
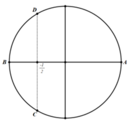
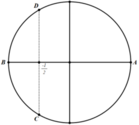
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng [ - π ; 0 ) , phương trình có đúng 2 nghiệm (là - π  và - 2 π 3 ).

Đáp án D.

Phương trình tương với:

cos x − 2 cos 2 x − 1 − 4 cos 3 x − 3 cos x + 1 = 0 ⇔ − 4 cos 3 x − 2 cos 2 x + 4 cos x + 2 = 0 ⇔ 2 t 3 + t 2 − − 2 t − 1 = 0 t = cos x ⇔ t 2 − 1 2 t + 1 = 0 ⇔ t = 1 t = − 1 t = − 1 2

Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng − π ; 0 , phương trình có đúng 2 nghiệm (là − π  và − 2 π 3 ).

Đáp án C

@Nguyễn Việt Lâm giúp em với ạ

a/ \(4cos^3x-3cosx-4\left(2cos^2x-1\right)+3cosx-4=0\)

\(\Leftrightarrow4cos^3x-8cos^2x=0\)

\(\Leftrightarrow4cos^2x\left(cosx-2\right)=0\)

\(\Leftrightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)

\(0< \frac{\pi}{2}+k\pi< 14\Rightarrow-\frac{1}{2}< k< \frac{14-\frac{\pi}{2}}{\pi}\Rightarrow k=\left\{0;1;2;3\right\}\)

\(\Rightarrow x=\left\{\frac{\pi}{2};\frac{3\pi}{2};\frac{5\pi}{2};\frac{7\pi}{2}\right\}\)

b/ Bạn coi lại đề, cái ngoặc thứ 2 thiếu \(\left(2cos\left(???\right)+cosx\right)\)

c/ Bạn coi lại đề, có 2 số hạng \(cos2x\) xuất hiện ở vế trái, cấp 3 chắc ko ai cho kiểu vậy đâu, nếu đúng thế thì người ta cộng luôn thành \(2cos2x\) cho rồi