Tính tổng của các đa thức:
M = x3 + xy + y2 – x2y2 – 2 và N = x2y2 + 5 – y2
Hãy tìm bậc của mỗi đa thức sau:
M = x2 – 2xy + 5x2 – 1
N = x2y2 – y2 + 5x2 – 3x2y + 5
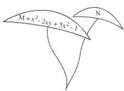
Rút gọn đa thức M ta có :
M = x2 – 2xy + 5x2 – 1 = (x2+ 5x2) – 2xy – 1 = 6x2 – 2xy – 1
Sau khi rút gọn, M có các hạng tử là:
6x2 có bậc 2
– 2xy có bậc 2
– 1 có bậc 0
Bậc của đa thức là bậc của hạng tử có bậc cao nhất
⇒ Đa thức M = x2 – 2xy + 5x2 – 1 có bậc 2.
Hãy tìm bậc của mỗi đa thức sau:
M = x2 – 2xy + 5x2 – 1
N = x2y2 – y2 + 5x2 – 3x2y + 5
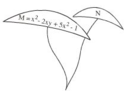
N = x2y2 – y2 + 5x2 – 3x2y + 5 có các hạng tử là
x2y2 có bậc 4 (vì biến x có bậc 2, biến y có bậc 2, tổng là 2 + 2 = 4)
– y2 có bậc 2
5x2 có bậc 2
– 3x2y có bậc 3 (vì biến x có bậc 2, biến y có bậc 1, tổng là 2 + 1 = 3)
5 có bậc 0
Bậc của đa thức là bậc của hạng tử có bậc cao nhất.
⇒ Đa thức N = x2y2 – y2 + 5x2 – 3x2y + 5 có bậc 4
Tính tổng của các đa thức:
P = x2y + xy2 – 5x2y2 + x3 và Q = 3xy2 – x2y + x2y2
Ta có: P = x2y + xy2 – 5x2y2 + x3 và Q = 3xy2 – x2y + x2y2
⇒ P + Q = (x2y + xy2 – 5x2y2 + x3) + (3xy2 – x2y + x2y2)
= x2y + xy2 – 5x2y2 + x3 + 3xy2 – x2y + x2y2
= x3 +(– 5x2y2 + x2y2)+ (x2y – x2y) + (xy2+ 3xy2)
= x3 – 4x2y2 + 0 + 4xy2
= x3 – 4x2y2 + 4xy2
Phân tích các đa thức sau thành nhân tử:
a) 3x - 3y + x 2 - y 2 ; b) x 2 -4 x 2 y 2 + y 2 + 2xy
c) x 6 - x 4 + 2 x 3 + 2 x 2 ; d) x 3 - 3x 2 +3x - 1 - y 3 .
a) (x - y)(x + y + 3). b) (x + y - 2xy)(2 + y + 2xy).
c) x 2 (x + l)( x 3 - x 2 + 2). d) (x – 1 - y)[ ( x - 1 ) 2 + ( x - 1 ) y + y 2 ].
Phân tích đa thức sau:
x2 + y2 - x2y2 + xy - x - y
Giúp mình với![]()
\(x^2+y^2-x^2y^2+xy-x-y\)
\(=\left(x^2-x^2y^2\right)+\left(y^2-y\right)+\left(xy-x\right)\)
\(=x^2\left(y-1\right)\left(-1-y\right)+y\left(y-1\right)+x\left(y-1\right)\)
\(=\left(y-1\right)\left(-x^2-x^2y+y+x\right)\)
\(=\left(y-1\right)\left[-x\left(x-1\right)-y\left(x-1\right)\left(x+1\right)\right]\)
\(=\left(y-1\right)\left(x-1\right)\left(-x-xy-y\right)\)
Bài 49 (trang 46 SGK Toán 7 tập 2): Hãy tìm bậc của mỗi đa thức sau:
M = x2 – 2xy + 5x2 – 1
N = x2y2 – y2 + 5x2 – 3x2y + 5
nếu có trong sách thì lên google
\(M=6x^2-2xy-1\left(bậc:2\right)\)
N có bậc 4
Lời giải:
a) Rút gọn đa thức M ta có :
M = x2 – 2xy + 5x2 – 1 = (x2+ 5x2) – 2xy – 1 = 6x2 – 2xy – 1
Sau khi rút gọn, M có các hạng tử là:
6x2 có bậc 2
– 2xy có bậc 2
– 1 có bậc 0
Bậc của đa thức là bậc của hạng tử có bậc cao nhất
⇒ Đa thức M = x2 – 2xy + 5x2 – 1 có bậc 2.
b) N = x2y2 – y2 + 5x2 – 3x2y + 5 có các hạng tử là
x2y2 có bậc 4 (vì biến x có bậc 2, biến y có bậc 2, tổng là 2 + 2 = 4)
– y2 có bậc 2
5x2 có bậc 2
– 3x2y có bậc 3 (vì biến x có bậc 2, biến y có bậc 1, tổng là 2 + 1 = 3)
5 có bậc 0
Bậc của đa thức là bậc của hạng tử có bậc cao nhất.
⇒ Đa thức N = x2y2 – y2 + 5x2 – 3x2y + 5 có bậc 4
phân tích đa thức sau thành nhân tử:
x2+y2-x2y2+xy-x-y
chịu rùi
bài này khó quá nguyen truong giang
chúc bn học tốt
nhae$
 hihi
hihi
x2 + y2 - x2y2 + xy - x - y
=(x2-x2y2)+(y2-y)+(xy-x)
=x2(1-y)(1+y)-y(1-y)-x(1-y)
=(1-y)(x2+x2y-x-y)
=(1-y)[(x2-y)+(x2-x)]
=(1-y)[y(x-1)(x+1)+x(x-1)]
=(1-y)(x-1)(xy+x+y)
Tính tổng của hai đa thức sau: 5x2y – 5xy2 + xy và xy – x2y2 + 5xy2
(5x2y – 5xy2 + xy) + (xy – x2y2 + 5xy2)
= 5x2y – 5xy2 + xy + xy – x2y2 + 5xy2
= 5x2y + (5xy2 – 5xy2) + (xy + xy) – x2y2
= 5x2y + 2xy – x2y2
Phân tích đa thức thành nhân tử:
x2 + y2 - x2y2 + xy - x - y
x2 + y2 - x2y2 + xy - x - y = (x2-x) + (y2-y) + (-x2y2 + xy) = x(x+1) + y(y+1) + xy(xy+1) = ( x+ y+ xy)( x + 1 + y + 1 + xy + 1)
\(x^2+y^2-x^2y^2+xy-x-y\)
\(=\left(x^2-x\right)+\left(y^2-y\right)+ \left(-x^2y^2+xy\right)\)
\(=x\left(x+1\right)+y\left(y+1\right)+xy\left(xy+1\right)\)
\(=\left(x+y+xy\right)\left(x+1+y+1+xy+1\right)\)