Đề là gì

Pt\(\Leftrightarrow x^3-x\left(m+2\right)-2m+4=0\)

\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+2-m\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x^2-2x+2-m=0\left(1\right)\end{matrix}\right.\)

Để pt ban đầu có 3 nghiệm pb khi pt (3) có hai nghiệm pb khác -2

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(-2\right)^2-2\left(-2\right)+2-m\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\10-m\ne0\end{matrix}\right.\)\(\Rightarrow m>1;m\ne10\)

Vây...

\(\Delta'=b'^2-ac=\left(m-1\right)^2-\left(m^2-3\right)=4-2m\)

Để pt có 2 nghiệm pb : \(m< 2\)

Theo định lí vi - et :

\(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1.x_2=m^2-3\end{matrix}\right.\)

Mà \(x_1=3x_2\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x_2=m-1\\3x^2_2=m^2-3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m-1}{4}\\x_2=\pm\dfrac{\sqrt{m^2-3}}{\sqrt{3}}\end{matrix}\right.\)

\(x^2-\left(m-2\right)x+m\left(m-3\right)=0\)

\(\Leftrightarrow x^2-\left(m-2\right)x+\left(m^2-3m\right)=0\) (*)

\(\Delta'=\left(m-2\right)^2-\left(m^2-3m\right)\)

\(=m^2-4m+4-m^2+3m\)

\(=4-m\). Để (*) có 2 nghiệm phân biệt suy ra \(\Delta'>0\)

\(\Rightarrow4-m>0\Rightarrow m< 4\)

Vậy với m=4 (*) có 2 nghiệm phân biệt

\(x-4\sqrt{x+3}+m=0\)

\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)

\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)

\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)

\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)

\(\Rightarrow f\left(0\right)=-3\)

\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)

\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)

Phương trình x 2 – 2(m – 3) x + 8 – 4m = 0 (a ; 1; b’ = −(m – 3); c = 8 – 4m)

Ta có

∆ ' =   ( m   –   3 ) 2   –   ( 8   –   4 m ) =   m 2   –   2 m   +   1   =   ( m   –   1 ) 2

S   =   x 1   +   x 2   =   2   ( m   –   3 ) ; P   =   x 1 .   x 2   =   8   –   4 m

Vì a = 1 ≠ 0 nên phương trình có hai nghiệm âm phân biệt  ⇔ Δ ' > 0 P > 0 S < 0

⇔ m − 1 2 > 0 2 m − 3 < 0 8 − 4 m > 0 ⇔ m ≠ 1 m < 3 m < 2 ⇔ m ≠ 1 m < 2

Vậy m < 2 và m ≠ 1 là giá trị cần tìm.

Đáp án: A

Phương trình m x 2 – 2(m – 2)x + 3(m – 2) = 0 (a = m; b = – 2(m – 2); c = 3(m – 2))

Ta có

∆ ' = ( m – 2 ) 2 = 3 m ( m – 2 ) = − 2 m 2 + 2 m + 4 = ( 4 – 2 m ) ( m + 1 )

P = x 1 .   x 2   = 3 m − 2 m

Phương trình có hai nghiệm phân biệt cùng dấu khi  a ≠ 0 Δ > 0 P > 0 ⇔ m ≠ 0 4 − 2 m m + 1 > 0 3 m − 2 m > 0

⇔ m ≠ 0 − 1 < m < 2 m > 2 m < 0 ⇒ − 1 < m < 0

Vậy −1 < m < 0 là giá trị cần tìm

Đáp án: C

Đặt f(x) =  x 3  – 3 x 2  (C1)

y = m ( C 2 )

Phương trình  x 3  – 3 x 2  – m = 0 có ba nghiệm phân biệt khi và chỉ khi ( C 1 ) và ( C 2 ) có ba giao điểm.

Ta có:

f′(x) = 3 x 2  − 6x = 3x(x − 2) = 0

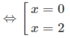
Bảng biến thiên:

Suy ra ( C 1 ) và ( C 2 ) cắt nhau tại 3 điểm khi -4 < m < 0

Kết luận : Phương trình   x 3  – 3 x 2  – m = 0 có ba nghiệm phân biệt với những giá trị của m thỏa mãn điều kiện: -4 < m < 0.

  ( m 2 + m + 3 ) x 2 + ( 4 m 2 + m + 2 ) x + m = 0  có a =   m 2   +   m   +   3 > 0, ∀m và có b =   4 m 2   +   m   +   2 > 0, ∀m, nên ab > 0, ∀m. Vì vậy không có giá trị nào của m để phương trình đã cho có hai nghiệm dương phân biệt.

1.

Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)

Pt trở thành:

\(4t=t^2-5+2m-1\)

\(\Leftrightarrow t^2-4t+2m-6=0\) (1)

Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)

2.

Để pt đã cho có 2 nghiệm:

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)

Khi đó:

\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)

\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)

\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)

3.

Nối AI kéo dài cắt BC tại D thì D là chân đường vuông góc của đỉnh A trên BC

\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{c}{b}\)

\(\Rightarrow\overrightarrow{BD}=\dfrac{c}{b}\overrightarrow{DC}\)

\(\Leftrightarrow\overrightarrow{ID}-\overrightarrow{IB}=\dfrac{c}{b}\left(\overrightarrow{IC}-\overrightarrow{ID}\right)\)

\(\Leftrightarrow b.\overrightarrow{IB}+\overrightarrow{c}.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}\) (1)

Mặt khác:

\(\dfrac{ID}{IA}=\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{a}{b+c}\)

\(\Leftrightarrow\left(b+c\right)\overrightarrow{ID}=-a.\overrightarrow{IA}\) (2)

(1); (2) \(\Rightarrow a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}-\left(b+c\right)\overrightarrow{ID}=\overrightarrow{0}\)