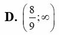Đặt f(x) = x 3 – 3 x 2 (C1)
y = m ( C 2 )
Phương trình x 3 – 3 x 2 – m = 0 có ba nghiệm phân biệt khi và chỉ khi ( C 1 ) và ( C 2 ) có ba giao điểm.
Ta có:
f′(x) = 3 x 2 − 6x = 3x(x − 2) = 0
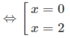
Bảng biến thiên:

Suy ra ( C 1 ) và ( C 2 ) cắt nhau tại 3 điểm khi -4 < m < 0
Kết luận : Phương trình x 3 – 3 x 2 – m = 0 có ba nghiệm phân biệt với những giá trị của m thỏa mãn điều kiện: -4 < m < 0.