Tìm ĐKXĐ của các biểu thức sau:
a) A = x + 2 x − 1 + 3 ; b) B = 2 x 2 + 1 − 3 : x − 1 2 x − 3 .
Tìm ĐKXĐ của các biểu thức :
a) A = \(\dfrac{1}{\sqrt{x^2-2x-1}}\)
b) B = \(\dfrac{1}{\sqrt{x-\sqrt{2x+1}}}\)
a) Biểu thức xác định `<=> x^2-2x-1>0`
`<=>(x^2-2x+1)-2>0`
`<=>(x-1)^2-(\sqrt2)^2>0`
`<=>(x-1+\sqrt2)(x-1-\sqrt2)>0`
`<=>` \(\left[{}\begin{matrix}x< 1-\sqrt{2}\\x>1+\sqrt{2}\end{matrix}\right.\)
`D=(-∞; 1-\sqrt2) \cup (1+\sqrt2 ; +∞)`
b) Biểu thức xác định `<=> x-\sqrt(2x+1)>0`
`<=> x>\sqrt(2x+1)`
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\2x+1\ge0\\x^2>2x+1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ge-\dfrac{1}{2}\\\left[{}\begin{matrix}x< 1-\sqrt{2}\\x>1+\sqrt{2}\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow x>1+\sqrt{2}\)
`D=(1+\sqrt2 ; +∞)`
Tìm ĐKXĐ của các biểu thức sau:
a) C = 5 x + 1 3 x − 2 − x 4 ; b) D = 3 3 x 2 + 1 + 1 4 : 5 x 3 − x .
cho biểu thức \(p=\left(1+\frac{1}{\sqrt{x}-1}\right)\frac{1}{x-\sqrt{x}}\)
a;Tìm ĐKXĐ và rút gọn P
b;Tim giá trị của p khi x = 25
bài2
Cho biểu thức \(A=\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{2}{\sqrt{x}+1}-\frac{2}{x-1}\)
a;tìm ĐKXĐ và rút gọn biể thức a
b; tìm a khi x=9
bài 3
cho biểu thức \(p=\left(\frac{3}{x-1}+\frac{1}{\sqrt{x}+1}\right)\div\frac{1}{\sqrt{x}+1}\)
a nếu ĐKXĐ và rút gọn biểu thức p
b tinh các giá trị của x để p =\(\frac{5}{4}\)
Bài 1 : Với : \(x>0;x\ne1\)
\(P=\left(1+\frac{1}{\sqrt{x}-1}\right)\frac{1}{x-\sqrt{x}}=\left(\frac{\sqrt{x}}{\sqrt{x}-1}\right).\sqrt{x}\left(\sqrt{x}-1\right)=x\)
Thay vào ta được : \(P=x=25\)
Bài 2 :
a, Với \(x\ge0;x\ne1\)
\(A=\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{2}{\sqrt{x}+1}-\frac{2}{x-1}=\frac{x+\sqrt{x}-2\sqrt{x}+2-2}{x-1}\)
\(=\frac{x-\sqrt{x}}{x-1}=\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}}{\sqrt{x}+1}\)
Thay x = 9 vào A ta được : \(\frac{3}{3+1}=\frac{3}{4}\)
Bài 3 : \(x\ge0;x\ne1\)
\(P=\left(\frac{3}{x-1}+\frac{1}{\sqrt{x}+1}\right):\frac{1}{\sqrt{x}+1}\)
\(=\left(\frac{2+\sqrt{x}}{x-1}\right).\left(\sqrt{x}+1\right)=\frac{\sqrt{x}+2}{\sqrt{x}-1}\)
b, Ta có : \(P=\frac{\sqrt{x}+2}{\sqrt{x}-1}=\frac{5}{4}\Rightarrow4\sqrt{x}+8=5\sqrt{x}-5\)
\(\Leftrightarrow\sqrt{x}=13\Leftrightarrow x=169\)(tmđk )
1, Cho biểu thức:
A =( √x/√x-1 + 2 / x- √x) : 1/√x-1
a.Tìm ĐKXĐ,rút gọn A.
b,Tìm GTNN của A.
2, Cho biểu thức:
B=(1/√x-1 + 1/√x+1).(1+ 1/√x)
a,Tim ĐKXĐ,rút gọn A.
b,Tìm x để {eq \x\le\ri(A)} > A
Cho các biểu thức sau:
A = \(\dfrac{x+3}{\sqrt{x}+1}\) và B = \(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{2\sqrt{x}}{1-x}\) với \(x\ge0;x\ne1\)
a) Rút gọn các biểu thức B
b) Cho \(P=B:A\). Với \(x>1\), tìm GTNN của biểu thức \(\dfrac{1}{P}\)
a.
\(B=\dfrac{\sqrt{x}+1+\sqrt{x}\left(\sqrt{x}-1\right)+2\sqrt{x}}{1-x}=\dfrac{\sqrt{x}+1+x-\sqrt{x}+2\sqrt{x}}{1-x}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b.
\(P=\dfrac{B}{A}=\dfrac{x+3}{\sqrt{x}+1}:\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{\left(x+3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{x+3}{\sqrt{x}-1}=\dfrac{x-1+4}{\sqrt{x}-1}\)
\(=\sqrt{x}+1+\dfrac{4}{\sqrt{x}-1}\)\(=\sqrt{x}-1+\dfrac{4}{\sqrt{x}-1}+2\)
Theo BĐT AM - GM ta có: \(\sqrt{x}-1+\dfrac{4}{\sqrt{x}-1}\ge2\sqrt{\left(\sqrt{x}-1\right)\dfrac{4}{\sqrt{x}-1}}=4\)
\(\Rightarrow\dfrac{1}{P}\ge6\Rightarrow Min_{\dfrac{1}{P}}=6\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=4\Rightarrow x=9\) (loại trường hợp \(\sqrt{x}-1=-2\))
Vậy GTNN của biểu thức \(\dfrac{1}{P}=6\) khi x = 9.
Cho A = \(\dfrac{\sqrt{x}}{2\sqrt{x}+1}\); B = \(\dfrac{1}{2\sqrt{x}+1}\)(ĐKXĐ: x ≥ 0; x ≠ \(\dfrac{1}{4}\)). Tìm tất cả các giá trị của x để biểu thức: P = 5A + B nguyên.
Lời giải:
$5A+B=\frac{5\sqrt{x}+1}{2\sqrt{x}+1}$
$2(5A+B)=\frac{10\sqrt{x}+2}{2\sqrt{x}+1}=\frac{5(2\sqrt{x}+1)-3}{2\sqrt{x}+1}=5-\frac{3}{2\sqrt{x}+1}$
$5A+B$ nguyên
$\Rightarrow 2(5A+B)$ nguyên
$\Leftrightarrow 5-\frac{3}{2\sqrt{x}+1}$ nguyên
$\Leftrightarrow \frac{3}{2\sqrt{x}+1}$ nguyên
Ta thấy: $\frac{3}{2\sqrt{x}+1}\leq 3$ với mọi $x\geq 0$ và $\frac{3}{2\sqrt{x}+1}>0$ với mọi $x\geq 0$
Do đó $\frac{3}{2\sqrt{x}+1}$ nguyên thì nhận các giá trị $1,2,3$
$\Leftrightarrow x=0; \frac{1}{16}; 1$
giúp mình bài này vs ạ
bài 1:so sánh các căn sau
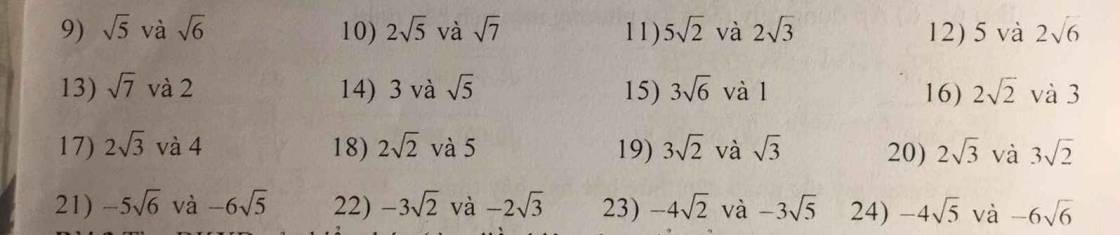
bài 2 :tìm ĐKXĐ của biểu thức (tìm đk của x để biểu thức sau có nghĩa)
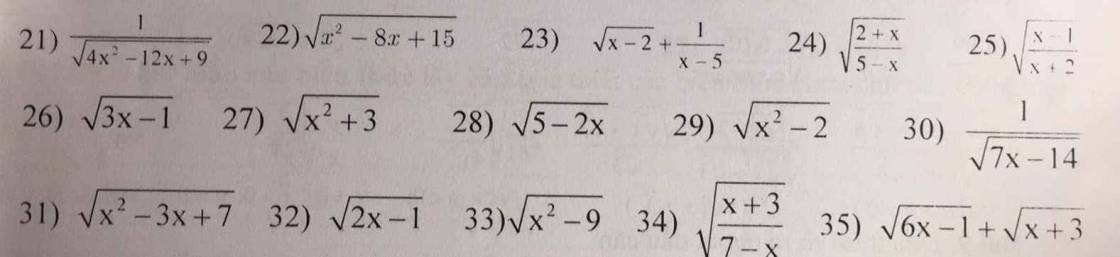
Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)
Chỉ đăng tối đa 10 - 15 câu hỏi thôi, câu trước GV nhắc bạn rồi mà giờ bạn vẫn còn đăng nữa thì nên bị xóa câu hỏi.
Bài 1: Giải phương trình sau:
\(2x^2+5+2\sqrt{x^2+x-2}=5\sqrt{x-1}+5\sqrt{x+2}\)
Bài 2: Cho biểu thức
\(P=\left(\frac{6x+4}{3\sqrt{3x^2}-8}-\frac{\sqrt{3x}}{3x+2\sqrt{3x}+4}\right).\left(\frac{1+3\sqrt{3x^2}}{1+\sqrt{3x}}-\sqrt{3x}\right)\)
a) Tìm ĐKXĐ và rút gọn biểu thức P
b) Tìm tất cả các giá trị nguyên của x để biểu thức P có giá trị nguyên
Bài 3: Cho biểu thức
\(A=\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{1-\frac{8}{x}+\frac{16}{x^2}}}\)
a) Tìm ĐKXĐ và rút gọn biểu thức A
b) Tìm tất cả các giá trị nguyên của x để biểu thức A có giá trị nguyên
a)Tìm giá trị nhỏ nhất của các biểu thức sau:
A = 25x2 - 10x + 11
B = (x - 3)2 + (11 - x)2
C = (x + 1)(x - 2)(x - 3)(x - 6)
b) Tìm giá trị lớn nhất của các các biểu thức sau:
D = 10x - 25x2 - 11
E = 19 - 6x - 9 x2
F = 2x - x2
c) Cho x và y thỏa mãn: x2 + 2xy + 6x + 2y2 + 8 = 0
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức B = x + y + 2024
\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)
b:
\(D=-25x^2+10x-1-10\)
\(=-\left(25x^2-10x+1\right)-10\)
\(=-\left(5x-1\right)^2-10< =-10\)
Dấu = xảy ra khi x=1/5
\(E=-9x^2-6x-1+20\)
\(=-\left(9x^2+6x+1\right)+20\)
\(=-\left(3x+1\right)^2+20< =20\)
Dấu = xảy ra khi x=-1/3
\(F=-x^2+2x-1+1\)
\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)
Dấu = xảy ra khi x=1