Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
a ) x 2 − 2 x + m = 0 b ) x 2 + 2 ( m − 1 ) x + m 2 = 0
Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
x2 + 2(m – 1)x + m2 = 0
Phương trình x2 + 2(m – 1)x + m2 = 0
Có a = 1; b = 2(m – 1); c = m2 nên b’ = m-1
⇒ Δ’ = b'2 – ac = (m – 1)2 – m2 = - 2m + 1.
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: 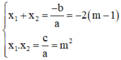
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m2
Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
x2 – 2x + m = 0;
Phương trình x2 – 2x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ’ = (-1)2 – 1.m = 1 – m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: 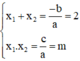
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
a) Tìm các giá trị của m để phương trình 2x2-(4m+3)x+2m-1=0 có 2 nghiệm phân biệt.
b) Tính tổng và tích 2 nghiệm theo m.
a) Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta=\left[-\left(4m+3\right)^2\right]-4.2.\left(2m-1\right)=16m^2+24m+9-16m+8=16m^2+8m+1+16=\left(4m+1\right)^2+16>0\)
với mọi giá trị của m.
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Vì phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m nên ta có: x1+x2= \(\dfrac{4m+3}{2}\)và x1.x2=\(\dfrac{2m-1}{2}\)
x^2-2mx+m^2+m-1=0 . a)tìm giá trị m để pt có nghiệm . b)tính tổng và tích hai nghiệm của phương trình theo m. c)tìm giá trị của m để hai nghiệm x1 và x2 của phương trình thỏa điều kiện x1^2+x2^2=2
Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích của nghiệm theo m.
a) x2 - 2x + m = 0; b) x2 + 2(m-1)x + m2 = 0.
a) Phương trình x2– 2x + m = 0 có nghiệm khi ∆' = 1 - m ≥ 0 hay khi m ≤ 1
Khi đó x1 + x2 = 2, x1 . x2 = m
b) Phương trình x2 – 2(m – 1)x + m2 = 0 có nghiệm khi
\(\text{∆}'=m^2-2m+1-m^2=1-2m\ge0\)' hay khi m \(\le\dfrac{1}{2}\)
Khi đó x1 + x2 = -2(m – 1), x1 . x2 = m2
a) Phương trình x2– 2x + m = 0 có nghiệm khi ∆' = 1 - m ≥ 0 hay khi m ≤ 1
Khi đó x1 + x2 = 2, x1 . x2 = m
b) Phương trình x2 – 2(m – 1)x + m2 = 0 có nghiệm khi
∆' = m2 - 2m + 1 – m2 = 1 – 2m ≥ 0 hay khi m ≤
Khi đó x1 + x2 = -2(m – 1), x1 . x2 = m2
Cho phương trình
x2+mx+2m-4=0
a Chứng tỏ phương trình trên luôn có nghiệm với mọi giá trị m
b Tính tổng và tích của 2 nghiệm theo m
c Tìm m để phương trình có 2 nghiệm x1,x2 thỏa mãn x1^2+x2^2=4 
a.
\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0;\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=2m-4\end{matrix}\right.\)
c.
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow m^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+4=0\Rightarrow m=2\)
a.\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0\)
=> pt luôn có nghiệm với mọi m
b.Theo hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1.x_2=2m-4\end{matrix}\right.\)
c.\(x_1^2+x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=4\)
\(\Leftrightarrow\left(-m\right)^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+8-4=0\)
\(\Leftrightarrow m^2-4m+4=0\)
\(\Leftrightarrow\left(m-2\right)^2=0\)
\(\Leftrightarrow m=2\)
cho pt \(mx^2-2mx+1=0\)
a) Tìm các giá trị của m để phương trình có nghiệm và tính nghiệm của phương trình theo m
b) Tìm các giá trị của m để phương trình có 2 nghiệm sao cho 1 nghiệm gấp đôi nghiệm kia
a)
+) Với m = 0 thay vào phương trình ta có: 1 = 0 => loại
+) Với m khác 0
\(\Delta'=m^2-m=m\left(m-1\right)\)
Để phương trình có nghiệm điều kiện là: \(m\left(m-1\right)\ge0\)
TH1: m \(\ge\)0 và m - 1 \(\ge\)0
<=> m \(\ge\) 0 và m \(\ge\)1
<=> m \(\ge\)1
TH2: m \(\le\) 0 và m - 1 \(\le\)0
<=> m \(\le\)0 và m \(\le\)1
<=> m \(\le\)0
Đối chiếu điều kiên m khác 0
Vậy m < 0 hoặc m \(\ge\)1
+) Tính nghiệm của phương trình theo m. Tự làm áp dụng công thức
b) Gọi \(x_1;x_2\) là hai nghiệm của phương trình
Theo định lí vi ét ta có:
\(x_1x_2=\frac{1}{m};x_1+x_2=\frac{2m}{m}=2\)
Không mất tính tổng quát ta g/s: \(x_1=2x_2\)
=> \(3x_2=2\Leftrightarrow x_2=\frac{2}{3}\)=> \(x_1=\frac{4}{3}\)
Ta có: \(\frac{4}{3}.\frac{2}{3}=\frac{1}{m}\)
<=> \(m=\frac{9}{8}\)( thỏa mãn a )
Thử lại thỏa mãn
Vậy m = 9/8
Cho phương trình bậc 2: (m - 1)x2 - 2mx + m + 1 = 0.
a) Tìm m, biết phương trình có nghiệm x = 0.
b) Xác định giá trị của m để phương trình có tích 2 nghiệm bằng 5, từ đó hãy tính tổng 2 nghiệm của phương trình.
a) Thay \(x=0\) vào phương trình ta có:
\(\left(m-1\right).0^2-2m.0+m+1=0.\\ \Leftrightarrow m+1=0.\\ \Leftrightarrow m=-1.\)
b) Ta có: \(\Delta'=m^2-\left(m-1\right)\left(m+1\right).\)
\(\Delta'=m^2-\left(m^2-1\right).\\ =m^2-m^2+1.\\ =1>0.\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt \(x_1;x_2.\)
Theo Viet: \(\left\{{}\begin{matrix}x_1.x_2=\dfrac{m+1}{m-1}.\\x_1+x_2=\dfrac{2m}{m-1}.\left(1\right)\end{matrix}\right.\)
Theo đề bài: \(x_1.x_2=5.\)
\(\Rightarrow\dfrac{m+1}{m-1}=5.\\ \Leftrightarrow m+1=5m-5.\\ \Leftrightarrow4m-6=0.\\ \Leftrightarrow m=\dfrac{3}{2}.\)
Thay \(m=\dfrac{3}{2}\) vào \(\left(1\right):\)
\(x_1+x_2=\) \(\dfrac{2.\dfrac{3}{2}}{\dfrac{3}{2}-1}=\dfrac{3}{\dfrac{1}{2}}=6.\)
Cho phương trình : x2 - 4mx +9(m-1)2 = 0
a. Xem xét với các giá trị nào của m thì phương trình trên có nghiệm ?
b. Giả sử x1, x2 là nghiệm của phương trình đã cho, hãy tính tổng và tích của chúng. Tìm một hệ thức giữa x1 và x2 không phụ thuộc vào m.
c. Xác định giá trị của m để hiệu các nghiệm của phương trình bằng 4.
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
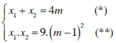
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
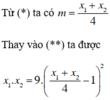
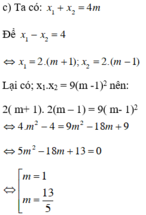
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành 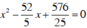 có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.