Cho hình lập phương A B C D . A ' B ' C ' D ' . Gọi M, N lần lượt là trung điểm của AD, BB'. Cosin của góc hợp bởi MN và AC' bằng
A. 2 3
B. 3 3
C. 5 3
D. 2 4
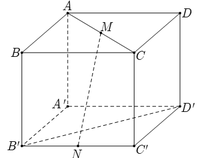
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B′C′ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B′D′ bằng
A. 5 a 5
B. a 3
C. 5 a
D. 3 a
cho hình thang ABCD (AB//CD)
a/ gọi M,N,P,Q lần lượt là trung điểm của AD ,BC,BD,AC .Chứng minh M,N,P,Q thẳng hàng .Tính MN ,PQ biết AB =a ,CD =b(a<b)
b/gọi I,J là trung điểm của AB,CD .Tứ giác IPJQ là hình gì
c/gọi A*B*C*D* lần lượt là trung điểm của AN ,BM,CM,DN.Chứng minh rằng A*B*C*D* là hình bình hành
Cho hình lập phương ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm của AB, B'C'. Góc giữa hai đường thẳng DM và A'N bằng A. 90° B. 60° C. 45° D. 30°
\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A
Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6) và ba điểm B, C, D cùng thuộc mặt phẳng (Oyz). Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Lập phương trình mặt phẳng (MNP)
A. x + 1 = 0
B. x - 1 = 0
C. y + z - 1 = 0
D. x = 1 + t, y = -2, z = 3
Đáp án B
* Tam giác ABC có MN là đường trung bình nên MN // BC (1)
Tam giác ACD có NP là đường trung bình nên NP // CD (2)
Từ (1) và (2) suy ra: (MNP) song song mp( BCD) hay (MNP) song song mp(Oyz).
* Mà mặt phẳng (Oyz) có 1 vecto pháp tuyến là i → (1; 0; 0) nên mặt phẳng (MNP) có VTPT i → (1; 0; 0).
* Điểm O(0; 0; 0). Gọi I(1; -2; 3) là trung điểm của AO. Suy ra; điểm I thuộc mặt phẳng (MNP).
* Phương trình mặt phẳng (MNP) là:
1(x- 1) + 0(y+ 2) + 0( z- 3) =0 hay x- 1= 0
Chọn B.
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Chọn D.
Dễ thấy A'A, B'M, D'N đồng quy tại S, SA' = 2a. Từ đó, ta tính được V S . A ' B ' D ' và V S . AMN . Suy ra tính được V H
cho hình lập phương ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm A'B' và BC. chứng minh MN vuông góc AC'
help pls
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, B'C', DD'. Hãy xác định thiết diện tạo bởi hình lập phương đã cho và mặt phẳng (MNP).
Cho tam giác ABC. Gọi M và N lần lượt là trung điểm của AB và AC. Vẽ điểm D và E sao cho N là trung điểm của BD và M là trung điểm của CE. Chứng minh rằng;
a) ∆ = ∆ AND CNB
b) AD = BC; AD // BC.
c) A là trung điểm của ED.
Các bạn giúp mình nhé. hình vẽ đại hơi xấu nha mọi người.
a: Xét ΔAND và ΔCNB có
NA=NC
\(\widehat{AND}=\widehat{CNB}\)
ND=NB
Do đó: ΔAND=ΔCNB
b: Xét tứ giác ABCD có
N là trung điểm của AC
N là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AD//BC và AD=BC
c: Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
SUy ra: AE//BC và AE=BC
mà AD//BC
và AD,AE có điểm chung là A
nên D,A,E thẳng hàng
mà AE=AD
nên A là trung điểm của ED
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN
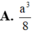
![]()