Tính tích phân I = ∫ - 1 1 f x d x biết rằng f x = 2 2017 x k h i x ≥ 0 2 - 2017 x k h i x < 0
A. I = 2 2018 - 2 2017 log 2 e
B. I = 2 2018 - 1 2017 log 2 e
C. I = 2 2018 - 1 2017 ln 2
D. I = 2 2017 - 1 2017 ln 2 .
PB
Những câu hỏi liên quan
Cho hàm số f(x) xác định và liên tục trên [0;1], thỏa mãn f'(x)=f'(1-x) với mọi x thuộc [0;1]. Biết rằng f(0)=1; f(1)=41. Tính tích phân I=\(\int_0^1f\left(x\right)dx\)
\(f'\left(x\right)=f'\left(1-x\right)\Rightarrow\int f'\left(x\right)dx=\int f'\left(1-x\right)dx\)
\(\Rightarrow f\left(x\right)=-f\left(1-x\right)+C\Rightarrow f\left(x\right)+f\left(1-x\right)=C\)
Thay \(x=0\Rightarrow f\left(0\right)+f\left(1\right)=C\Rightarrow C=42\)
\(\Rightarrow\int\limits^1_0\left[f\left(x\right)+f\left(1-x\right)\right]dx=\int\limits^1_042dx=42\)
Xét \(I=\int\limits^1_0f\left(1-x\right)dx\)
Đặt \(1-x=u\Rightarrow dx=-du;\left\{{}\begin{matrix}x=0\Rightarrow u=1\\x=1\Rightarrow u=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1f\left(u\right).\left(-du\right)=\int\limits^1_0f\left(u\right).du=\int\limits^1_0f\left(x\right)dx\)
\(\Rightarrow2\int\limits^1_0f\left(x\right)dx=42\Rightarrow\int\limits^1_0f\left(x\right)dx=21\)
Đúng 4
Bình luận (0)
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(x) + f(
π
3
-
x
)
1
2
sin
x
cos
x
(
8
cos
3
x
+
1
)
,
∀
x
∈...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(x) + f( π 3 - x )= 1 2 sin x cos x ( 8 cos 3 x + 1 ) , ∀ x ∈ R Biết tích phân I= ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I= a b ln c d ; a , b , c , d ∈ Z và các phân số a b ; c d là các phân số tối giản. Tính S= a 3 + a b - c + d
Cho hàm số f(x) liên tục trên R và thỏa mãn
f
(
x
)
+
f
π
3
-
x
1
3
sin
x
cos
x
(
8
cos...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và thỏa mãn f ( x ) + f π 3 - x = 1 3 sin x cos x ( 8 cos 3 x + 1 ) . Biết tích phân I = ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I = a b ln c d và các phân số là các phân số tối giản. Tính S = a 3 + a b - c + d
A. S=6
B. S=3
C. S=5
D. S=7
Cho hàm số y f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y f(x) tại các điểm có hoành độ x -1, x 0, x 1 lần lượt tạo với chiều dương của trục Ox các góc
30
o
,
45
o
,
60
o
Tính tích phân
I
∫
-
1
0
f...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y = f(x) tại các điểm có hoành độ x = -1, x = 0, x = 1 lần lượt tạo với chiều dương của trục Ox các góc 30 o , 45 o , 60 o
Tính tích phân I = ∫ - 1 0 f ' x . f ' ' x dx + 4 ∫ 0 1 f ' x 3 . f ' ' x dx .
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số y f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y f(x) tại các điểm có hoành độ x -1, x0, x1 lần lượt tạo với chiều dương của trục Ox các góc
30
o
,
45
o
,
60
o
Tính tích phân
I
∫
-
1
0
f...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y = f(x) tại các điểm có hoành độ x = -1, x=0, x=1 lần lượt tạo với chiều dương của trục Ox các góc 30 o , 45 o , 60 o
Tính tích phân I = ∫ - 1 0 f ' x . f ' ' x dx + 4 ∫ 0 1 f ' x 3 . f ' ' x dx .
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số yf(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx1, x ϵ [0;π/3] và f(0)1. Tính tích phân
I
∫
0
π
3
f
x
d
x
A. 1/2 + π/3 B.
3
+
1
2
C. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số y f(x) xác định và có đạo hàm trên đoạn [0;2]. Biết rằng f(2) -3 và
∫
0
2
x
f
(
x
)
d
x
-
4
Tính tích phân
I
∫
0
2
f
(
x
)
d
x
A. I 2. B. I 0. C. I -7. D. I -2.
Đọc tiếp
Cho hàm số y = f(x) xác định và có đạo hàm trên đoạn [0;2]. Biết rằng f(2) = -3 và ∫ 0 2 x f ' ( x ) d x = - 4 Tính tích phân I = ∫ 0 2 f ( x ) d x
A. I = 2.
B. I = 0.
C. I = -7.
D. I = -2.
Đáp án D
Phương pháp:
Sử dụng công thức từng phần.
Cách giải:
Ta có :
Đúng 0
Bình luận (0)
Cho f(x) xác định và liên tục trên
ℝ
, biết f(1)2, f(3)4. Tính tích phân
I
∫
1
2
2
f
x
−
x
d
x
.
A. I 0. B. I 1. C. I -2. D I 2.
Đọc tiếp
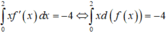
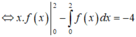
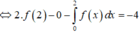
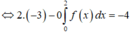
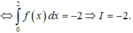
Cho f(x) xác định và liên tục trên ℝ , biết f(1)=2, f(3)=4. Tính tích phân I = ∫ 1 2 2 f ' x − x d x .
A. I = 0.
B. I = 1.
C. I = -2.
D I = 2.
Cho hàm số f(x) là hàm số lẻ, liên tục trên [-4;4]. Biết rằng
∫
-
2
0
f
(
-
x
)
d
x
2
và
∫
1
2
f
(
-
2
x
)
d
x
4
. Tính tích phân I
∫
0
4...
Đọc tiếp
Cho hàm số f(x) là hàm số lẻ, liên tục trên [-4;4]. Biết rằng ∫ - 2 0 f ( - x ) d x = 2 và ∫ 1 2 f ( - 2 x ) d x = 4 . Tính tích phân I= ∫ 0 4 f ( x ) d x
Cho hàm số f(x) nhận giá trị dương, có đạo hàm liên tục trên [0;2]. Biết f(0) 1 và
f
x
f
2
-
x
e
2
x
2
-...
Đọc tiếp
Cho hàm số f(x) nhận giá trị dương, có đạo hàm liên tục trên [0;2]. Biết f(0) =1 và f x f 2 - x = e 2 x 2 - 4 x với mọi x ∈ [ 0 ; 2 ] . Tính tích phân I = ∫ 0 2 x 3 - 3 x 2 f ' x f x dx .
A. I = -14/3
B. I = -32/5
C. I = -16/3
D. I = -16/5
