Cho hình vuông ABCD cạnh a. Giá trị của A B → . A C → là
A. a 2
B. 1 2 a 2
C.- 1 2 a 2
D. − 3 2 a 2
Cho hình lập phương ABCD. A’B’C’D’ có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’. Kết quả tính diện tích toàn phần S t p của hình nón đó có dạng bằng πa 2 4 b + c với b, c là hai số nguyên dương và b > 1. Tính giá trị của bc?
A. bc = 5
B. bc = 8
C. bc = 15
D. bc = 7
Đáp án A
Khối nón cần tìm có chiều cao h = a, bán kính đáy r = a 2 ⇒ l = h 2 + r 2 = a 5 2
Diện tích toàn phần của hình nón là S t p = S x q + S d = πrl + πr 2 = π . a 2 . a 5 2 + π a 2 2 .
= πa 2 4 5 + 1 = πa 2 4 b + c . Vậy b = 5 c = 1 → b c = 5 .
Cho hình vuông ABCD có cạnh a. Giá trị của biểu thức vectoBC*(2*vectoAD - vectoAB) theo a là bao nhiêu ?
ta có \(\overrightarrow{BC}\cdot\left(2\overrightarrow{\cdot AD}-\overrightarrow{AB}\right)=2\cdot\overrightarrow{BC}\cdot\overrightarrow{AD}-\overrightarrow{BC}\cdot\overrightarrow{AB}=2a^2\)
(Do BC và AD cùng hướng, BC và AB vuông góc với nhau)
Cho hình chóp S. ABCD có tất cả các cạnh bên và cạnh đáy đều bằng a và ABCD là hình vuông. Gọi M là trung điểm của CD. Giá trị M S → . C B → bằng
A. a 2 2
B. - a 2 2
C. a 2 3
D. 2 a 2 2
Cho Hình vuông ABCD cạnh a. M là trung điểm của AB . Tính giá trị biểu thức : (AB +AD)(BD+BC)
Cho hình vuông ABCD cạnh a . Tính giá trị các biểu thức sau:
a) \(\overrightarrow{AB}.\overrightarrow{AC}\)
b)\(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
c)\(\overrightarrow{AB}.\overrightarrow{BD}\)
d) \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)\)
e) \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
a, \(AC=\dfrac{AB}{sin45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a\sqrt{2}.cos45^o=a^2\)
b, \(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=\overrightarrow{AC}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{AC}.\overrightarrow{BD}+\overrightarrow{AC}.\overrightarrow{BC}\)
\(=AC.BD.cos90^o+AC.AD.cos45^o\)
\(=a\sqrt{2}.a\sqrt{2}.0+a\sqrt{2}.a.\dfrac{\sqrt{2}}{2}=a^2\)
c, \(\overrightarrow{AB}.\overrightarrow{BD}=AB.BD.cos135^o=-a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=-a^2\)
d, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{BC}.\left(\overrightarrow{AD}+\overrightarrow{BD}\right)\)
\(=\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{BC}.\overrightarrow{BD}\)
\(=AD^2+BC.BD.cos45^o\)
\(=a^2+a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=2a^2\)
e, \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
\(=\left(\overrightarrow{AC}+\overrightarrow{AC}\right)\left(\overrightarrow{DB}+\overrightarrow{DB}\right)\)
\(=4.\overrightarrow{AC}.\overrightarrow{DB}=4.AC.DB.cos90^o=0\)
Cho hình vuông ABCD có cạnh bằng a, M là trung điểm của BC. Tính giá trị đúng của cos AMD.
Theo định lý cosin ta có
\(AD^2=AM^2+MD^2-2.MA.MD.cos\widehat{ÀMD}\)
Xé \(\Delta ABM\)có \(BM=\frac{a}{2}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
Xét \(\Delta DCM\)có \(CM=\frac{a}{2}\)
\(\Rightarrow DM=\sqrt{DC^2+CM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
\(\Rightarrow\cos\widehat{AMD}=\frac{AM^2+MD^2-AD^2}{2.MA.MD}=\frac{\frac{5a^2}{4}+\frac{5a^2}{4}-a^2}{\frac{\sqrt{5}a}{2}.\frac{\sqrt{5}a}{2}}=\frac{3}{5}\)
Vậy \(\cos\widehat{AMD}=\frac{3}{5}\)
Cho hình chóp S.ABCDcó đáy ABCD là hình vuông cạnh a, S A ⊥ A B C D và S A = x . Tìm giá trị của x để góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 .
A. x = 2 a .
B. x = 3 a 2 .
C. x = a 2 .
D. x = a .
Đáp án D
Hạ H, K lần lượt là hình chiếu vuông góc của A xuống SB và SD.
Ta có:
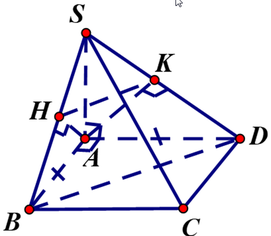
A H ⊥ S B A H ⊥ B C ⇒ A H ⊥ S B C . Tương tự A K ⊥ S D C
Như vậy S B C , S D C ^ = A H , A K ^ = H A K ^
Ta có Δ S A B = Δ S A D suy ra A H = A K . Vì góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 nên ΔAHK đều.
Ta có S H S B = S K S D = H K B D , mà S H S B = S A 2 S B 2 = x 2 x 2 + a 2 = K H a 2 suy ra K H = a 2 x 2 x 2 + a 2 .
Ta lại có 1 A H 2 = 1 S A 2 + 1 A B 2 = a 2 + x 2 a 2 x 2 suy ra A H 2 = a 2 x 2 a 2 + x 2 .
ΔAHK đều nên ta có
K H 2 = A H 2 ⇔ a 2 x 2 x 2 + a 2 2 = a 2 x 2 a 2 + x 2 ⇔ x = a .
Vậy x = a thì góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 .
Cho hình vuông ABCD cạnh a. M là trung điểm của AB, Tính giá trị các biểu thức sau: ( A B → + A D → ) . ( B D → + B C → )
A. a2
B. –a2
C. 2a2
D. Đáp án khác
Chọn A.
Theo quy tắc hình bình hành ta có ![]()
Do đó
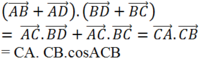
(![]() vì AC và BD vuông góc với nhau)
vì AC và BD vuông góc với nhau)
Mặt khác ![]() và theo định lý Pitago ta có:
và theo định lý Pitago ta có:
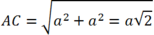
Suy ra ![]()
![]()