Cho n là nghiệm của C n 1 + C n n - 1 = 4040 . Khi đó tổng S = 2 1 - 1 1 C n 0 + 2 2 - 1 2 C n 1 + 2 3 - 1 3 C n 2 + . . . + 2 n + 1 - 1 n + 1 C n n bằng

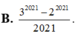
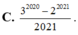
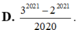
Chứng minh rằng:
a) Số các nghiệm tự nhiên của phương trình \(x_1+x_2+...+x_m=n\left(n,m\in N\cdot\right)\) là \(C^n_{m+n-1}\).
b) Số các nghiệm nguyên dương của phương trình \(x_1+x_2+...+x_m=n\left(m\le n;m,n\in N\cdot\right)\) là \(C^{m-1}_{n-1}\).
Em có tìm một số lời giải cho bài toán này nhưng vẫn không hiểu lắm, mong ai đó có lời giải chi tiết và dễ hiểu :)
Bài toán chia kẹo kinh điển đây mà.
Trước hết chúng ta đếm 1 chút theo kiểu lớp 1 lớp 2 gì đó: có 1 đoạn thẳng, cần chia đoạn thẳng ấy làm 3 phần, vậy cần chấm lên đoạn thẳng ấy mấy điểm? Câu trả lời rõ ràng là 2 điểm. Cần chia 1 con cá thành 3 khúc, ta cần 2 nhát cắt; cần ngăn 4 con cọp xếp hàng ngang để chúng đỡ cắn nhau, ta cần 3 vách ngăn. Hay để chia 1 đối tượng làm n phần, ta cần dùng n-1 vách ngăn để chia nó ra, Như thế này:
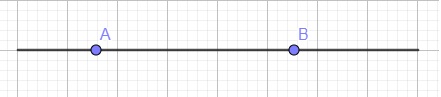
Bây giờ có số tự nhiên n, ta phân tích nó như sau:
\(n=1+1+1+...+1+1+1\)
Giả sử ta "vách ngăn" vào một vài vị trí giữa các số 1, kiểu thế này:
\(1+1+\left|1+1+1\right|+1+|1+1+...+1\)
Rõ ràng với 3 vách ngăn trên, ta chia n thành 3+1=4 phần, mỗi phần đều có giá trị nguyên dương, lần lượt là 2,3,1,n-6.
Bây giờ cần chia dãy \(1+1+...+1\) trên thành m phần, vậy cần đặt bao nhiêu vách ngăn? Cũng như ban đầu đã phân tích, ta cần đặt \(m-1\) tấm vách ngăn.
Ta có bao nhiêu vị trí để đặt \(m-1\) vách ngăn nói trên? Có n số 1, ta sẽ có \(n-1\) vị trí đặt vách ngăn, sao cho giữa 2 vách ngăn có ít nhất một số 1 (hay giữa 2 vách ngăn luôn là 1 giá trị nguyên dương).
Tóm lại, để chia dãy tổng \(1+1+...+1\) (n số hạng) thành m phần, sao cho mỗi phần chứa ít nhất một số 1, ta cần đặt \(m-1\) tấm vách ngăn vào \(n-1\) vị trí khả dĩ. Như vậy, ta có \(C_{n-1}^{m-1}\) cách.
Hiển nhiên, giá trị của mỗi phần (tức là tổng các số 1 trong phần đó) chính là giá trị nghiệm \(x_i\) của pt \(\sum\limits^m_{i=1}x_i=n\). Vậy pt có \(C_{n-1}^{m-1}\) nghiệm nguyên dương.
//Bay giờ tới nghiệm tự nhiên thì đơn giản, số tự nhiên khác số nguyên dương đúng 1 số 0, bây giờ ta "loại" nó đi là ra bài toán bên trên. Bằng cách đặt \(y_1=x_1+1;y_2=x_2+1...;y_m=x_m+1\), ta đảm bảo \(y_i\) luôn nguyên dương khi \(x_i\) tự nhiên.
Khi đó:
\(y_1+y_2+...+y_m=\left(x_1+1\right)+\left(x_2+1\right)+...+\left(x_m+1\right)\)
\(=\left(x_1+x_2+...+x_m\right)+m=n+m\)
Quay về bài trên, ta có pt \(y_1+y_2+...+y_m=n+m\) có \(C_{n+m-1}^{m-1}\) nghiệm.
Ứng với mỗi \(y_i\) cho đúng 1 giá trị \(x_i=y_i-1\) tương ứng, do đó pt:
\(\sum\limits^m_{i=1}x_i=n\) có \(C_{n+m-1}^{m-1}\) nghiệm tự nhiên
Công thức đầu của em có vẻ bị sai :D
C35 Cho n là số nguyên dương lẻ , thõa mãn 5 C ¹N - C² N =15 . Tìm hệ số của x² trong khai triển nhị thức Niuton ( 2x+ 1/x²)^n A. 60 B. 90 C. 80 D .110 C14: số Nghiệm của pt √3x+5=2 là A. 3 B. 0 C. 2 D. 1 Giúp cho e
cho các ptrinh x2+bx+c =0(1)
x2+mx+n=0(2)
trong đó b,c,m,n là các số khác 0 biết b,c là các nghiệm của pt (2) và m,n là các nghiệm của pt (1)
cmr: b2+c2+m2+n2=10
Áp dụng hệ thức Vi-et,ta có :
m + n = -b ( 1 )
mn = c ( 2 )
b + c = -m ( 3 )
bc = n ( 4 )
từ ( 1 ) và ( 3 ) suy ra c = n
thay vào ( 2 ) và ( 4 ), ta được b = m = 1
từ đó tìm được c = n = -2
Do đó b2 + c2 + m2 + n2 = 10
chi tiết bạn tự làm
Cho phương trình
x^2-x+m=0 ( 1) (m là tham số)
a, Giải phương trình khi m=-6
b, tìm m để pt (1) có nghiệm
c,Tìm n sao cho pt x^2-97x+n=0 (2) ( n là tham số) có các nghiệm là lũy thừa bậc 4 của các nghiệm phương trình (1)
CÂU C
HELP>>>
Gọi x1,x2 là hai nghiệm của pt (1) : x^2 - 97x + a = 0 và x3,x4 là 2 nghiệm của pt (2) : x^2 - x + b = 0
Theo hệ thức Vi-ét :
x1 + x2 = 97 và x1.x2 = a
x3 + x4 = 1 và x3.x4 = b
Theo đề bài :
* x1 + x2 = x3^4 + x4^4
<=> x1 + x2 = (x3^2 + x4^2)^2 - 2.(x3.x4)^2
<=> x1 + x2 = [(x3 + x4)^2 - 2.x3.x4]^2 - 2(x3.x4)^2
<=> 97 = (1 - 2b)^2 - 2b^2
<=> 2b^2 - 4b - 96 = 0 (1)
* x1.x2 = (x3.x4)^4
<=> b^4 = a (2)
Từ (1) được b = 8 hoặc b = -6
Suy ra a = 4096 hoặc a = 1296
Thử lại nhận a = 1296
Nguồn: https://vn.answers.yahoo.com/question/index?qid=20130328075420AAV3DV4
omg thanks rapton321
mik viết mà nó ko hiện lên
viết đề mà ko có
Tìm giá trị của m,n sao cho mỗi hệ pt ẩn x, y sau đây:
a, {2mx + (1-n)y = m+n+1
{(m+1)x + (m+n)y = 3 có nghiệm (2;1)
b, {3mx - (n+1)y = 93
{nx + 1my = -3 có nghiệm (1;-5)
Cho pt: (m-1)x4 + 2x2 -3 = 0. Tìm điều kiện của m để pt:
a) Vô nghiệm
b) Có 1 nghiệm
c) Có 2 nghiệm phân biệt
d) Có 3 nghiệm phân biệt
e) Có 4 nghiệm phân biệt
Đặt \(x^2=t\ge0\Rightarrow\left(m-1\right)t^2+2t-3=0\) (1)
Với \(m=1\Rightarrow t=\frac{3}{2}\)
Với \(m\ne1\Rightarrow\Delta'=1+3\left(m-1\right)=3m-2\)
a/ \(m=1\) ko thỏa mãn
Để pt vô nghiệm \(\Rightarrow\Delta'< 0\Rightarrow m< \frac{2}{3}\) hoặc (1) có 2 nghiệm đều âm
\(\Rightarrow\left\{{}\begin{matrix}t_1+t_2=\frac{2}{1-m}< 0\\t_1t_2=\frac{3}{1-m}>0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn
Vậy \(m< \frac{2}{3}\)
b/ Để pt có đúng 1 nghiệm \(\Leftrightarrow\left(1\right)\) có đúng 1 nghiệm \(t=0\Rightarrow-3=0\) (vô lý)
Vậy ko tồn tại m thỏa mãn
c/ Để pt có 2 nghiệm pb \(\Rightarrow\left(1\right)\) có đúng 1 nghiệm dương
\(m=1\) thỏa mãn
Với \(m\ne1\):
TH1: \(\Delta'=0\Rightarrow m=\frac{2}{3}\Rightarrow t=\frac{1}{1-m}=3>0\) thỏa mãn
TH2: \(\left\{{}\begin{matrix}\Delta'>0\\t_1t_2< 0\end{matrix}\right.\) \(\Rightarrow\frac{3}{1-m}< 0\Rightarrow1-m< 0\Rightarrow m>1\)
Vậy: \(\left\{{}\begin{matrix}m=\frac{2}{3}\\m\ge1\end{matrix}\right.\)
d/ Để pt đã cho có 3 nghiệm pb \(\Leftrightarrow\left(1\right)\) có 1 nghiệm bằng 0 và 1 nghiệm dương
\(\Rightarrow-3=0\) (vô lý)
Không tồn tại m thỏa mãn
e/ Để pt có 4 nghiệm pb \(\Leftrightarrow\left(1\right)\) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}3m-2>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>\frac{2}{3}\\\frac{2}{1-m}>0\\\frac{3}{1-m}>0\end{matrix}\right.\)
\(\Rightarrow\frac{2}{3}< m< 1\)
Cho pt x^2 -x +m=0 (1) (m là tham số)
a) tìm m để pt (1) có nghiệm
b) tìm n để pt x^2-97x+n=0 (2)
(n là tham số) có các nghiệm là lũy thừa bậc 4 của các nghiệm của phương trình (1)
a/ \(\Delta=1-4m\ge0\Rightarrow m\le\frac{1}{4}\)
Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m\end{matrix}\right.\)
b/ \(\Delta=97^2-4n\ge0\Rightarrow n\le\frac{9409}{4}\)
Gọi \(a;b\) là các nghiệm của (2) \(\Rightarrow\left\{{}\begin{matrix}a+b=97\\ab=n\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}a=x_1^4\\b=x_2^4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a+b=x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2\\ab=\left(x_1x_2\right)^4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2\left(x_1x_2\right)^2\\ab=\left(x_1x_2\right)^4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=\left(1-2m\right)^2-2m^2=2m^2-4m+1\\ab=m^4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2m^2-4m+1=97\\n=m^4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=8\\m=-6\end{matrix}\right.\\n=m^4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}n=4096\left(l\right)\\n=1296\end{matrix}\right.\)
X*2-(2N-1)X+n(n-1) =0
a, giải phương trình khi n =2
b,cmr pt trên luôn có 2 nghiệm phân biệt với mọi n
c,cmr x1,x2 là 2 nghiệm của phương trình , sao cho x1*2-2x2 +3 luôn lớn hơn hoặc bằng 0 với mọi n
Cho phương trình \(x^2+bx+c=0\) (1) và phương trình x^2+mx+n=0 (2) (b;c;m;n\(\ne\)0). Cho biết b;c là 2 nghiệm của pt(2) và m;n là 2 nghiệm của pt(1). Chứng minh b^2+c^2+m^2+n^2=10