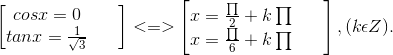Chọn C

Ta có: nên (1) và (2) có nghiệm.

Cách 1:

Xét: nên (3) vô nghiệm.

Cách 2:

Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là:

(vô lý) nên (3) vô nghiệm.

Cách 3:

Vì 

nên (3) vô nghiệm.

3.

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=cos3x\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=sin\left(\dfrac{\pi}{2}-3x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{2}-3x+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

câu 2 mình sửa lại đề bài một chút là: sin(cosx)=1 ạ

1.

\(sin\left(sinx\right)=0\)

\(\Leftrightarrow sinx=k\pi\) (1)

Do \(-1\le sinx\le1\Rightarrow-1\le k\pi\le1\)

\(\Rightarrow-\dfrac{1}{\pi}\le k\le\dfrac{1}{\pi}\Rightarrow k=0\) do \(k\in Z\)

Thế vào (1)

\(\Rightarrow sinx=0\Rightarrow x=n\pi\)

2.

\(sin\left(cosx\right)=1\Leftrightarrow cosx=\dfrac{\pi}{2}+k2\pi\)

Do \(-1\le cosx\le1\Rightarrow-1\le\dfrac{\pi}{2}+k2\pi\le1\)

\(\Rightarrow-\dfrac{1}{2\pi}-\dfrac{1}{4}\le k\le\dfrac{1}{2\pi}-\dfrac{1}{4}\) 

\(\Rightarrow\) Không tồn tại k thỏa mãn

Pt vô nghiệm

Đáp án đúng : A

\(sin\left(2x+\dfrac{\Omega}{2}\right)=sin\left(x-\dfrac{\Omega}{3}\right)\)

=>\(\left[{}\begin{matrix}2x+\dfrac{\Omega}{2}=x-\dfrac{\Omega}{3}+k2\Omega\\2x+\dfrac{\Omega}{2}=\Omega-x+\dfrac{\Omega}{3}+k2\Omega\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=-\dfrac{5}{6}\Omega+k2\Omega\\3x=\dfrac{4}{3}\Omega-\dfrac{1}{2}\Omega+k2\Omega\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=-\dfrac{5}{6}\Omega+k2\Omega\\x=\dfrac{5}{18}\Omega+\dfrac{k2\Omega}{3}\end{matrix}\right.\)

Lời giải:

$\sin (2x+\frac{\pi}{2})=\sin (x-\frac{\pi}{3})$

\(\Rightarrow \left[\begin{matrix}\ 2x+\frac{\pi}{2}=x-\frac{\pi}{3}+2k\pi\\ 2x+\frac{\pi}{2}=\pi -(x-\frac{\pi}{3})+2k\pi\end{matrix}\right.\)

\(\Rightarrow \left[\begin{matrix}\ x=\pi (2k-\frac{5}{6})\\ x=\frac{1}{3}\pi (\frac{5}{6}+2k)\end{matrix}\right.\) với $k$ nguyên bất kỳ.

a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos²x ta được phương trình tương đương 2tan²x + tanx - 3 = 0.

Đặt t = tanx thì phương trình này trở thành

2t² + t - 3 = 0 ⇔ t ∈ {1 ; }.

Vậy

b) Thay 2 = 2(sin²x + cos²x), phương trình đã cho trở thành

3sin²x - 4sinxcosx + 5cos²x = 2sin²x + 2cos²x

⇔ sin²x - 4sinxcosx + 3cos²x = 0

⇔ tan²x - 4tanx + 3 = 0

⇔

⇔ x = + kπ ; x = arctan3 + kπ, k ∈ Z.

c) Thay sin2x = 2sinxcosx ; = (sin²x + cos²x) vào phương trình đã cho và rút gọn ta được phương trình tương đương

sin²x + 2sinxcosx - cos²x = 0 ⇔ tan²x + 4tanx - 5 = 0 ⇔

⇔ x = + kπ ; x = arctan(-5) + kπ, k ∈ Z.

d) 2cos²x - 3√3sin2x - 4sin²x = -4

⇔ 2cos²x - 3√3sin2x + 4 - 4sin²x = 0

⇔ 6cos²x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0

⇔