Nếu lim x → 1 f ( x ) - 5 x - 1 = 2 và lim x → 1 g ( x ) - 1 x - 1 = 3 thì lim x → 1 f ( x ) . g ( x ) + 4 - 3 x - 1 bằng
A. 17 6
B. 23 7
C.7
D.17
Nếu \(lim\) (x->1) \(\dfrac{f\left(x\right)-5}{x-1}=2\) và lim (x->1) \(\dfrac{g\left(x\right)-1}{x-1}=3\) thì lim (x->1) \(\dfrac{\sqrt{f\left(x\right).g\left(x\right)+4}-3}{x-1}\) bằng mấy
Do \(x-1\rightarrow0\) khi \(x\rightarrow1\) nên \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-5}{x-1}=2\) hữu hạn khi và chỉ khi \(f\left(x\right)-5=0\) có nghiệm \(x=1\)
\(\Leftrightarrow f\left(1\right)-5=0\Rightarrow f\left(1\right)=5\)
Tương tự ta có \(g\left(1\right)=1\)
Do đó: \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{f\left(x\right).g\left(x\right)+4}-3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right).g\left(x\right)-5}{\left(x-1\right)\left(\sqrt{f\left(x\right).g\left(x\right)+4}+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-5\right].g\left(x\right)+5\left[g\left(x\right)-1\right]}{\left(x-1\right)\left(\sqrt{f\left(x\right).g\left(x\right)+4}+3\right)}\)
\(=\left(2.1+5.3\right).\dfrac{1}{\sqrt{5.1+4}+3}=\dfrac{17}{6}\)
nếu lim f(x)=L>0, lim g(x)=-vô cùng thì kết quả của giới hạn lim f(x).g(x) là:
A/ - vô cùng
B/ 0
C/ + vô cùng
D/ L
Biết lim x -> +∞ f(x) = M ;lim x -> +∞ g(x) = 0 Chọn khẳng định đúng? A. Lim x -> +∞ f(x)/g(x)= +∞ B. Lim x -> +∞ = f(x)/g(x)= -∞ C. Lim x -> +∞ f(x)/g(x)=0 D. Limx -> +∞ [g(x).f(x)]=0
Cho hai hàm số \(f\left( x \right) = {x^2} - 1,g\left( x \right) = x + 1.\)
a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
b) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
c) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
d) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
e) Tính \(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}}\)và so sánh \(\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\)
a) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - 1} \right) = \mathop {\lim }\limits_{x \to 1} {x^2} - \mathop {\lim }\limits_{x \to 1} 1 = {1^2} - 1 = 0\)
\(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to 1} x + \mathop {\lim }\limits_{x \to 1} 1 = 1 + 1 = 2\)
b) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x} \right) = {1^2} + 1 = 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 + 2 = 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
c) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - x - 2} \right) = {1^2} - 1 - 2 = - 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 - 2 = - 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
d) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left[ {\left( {{x^2} - 1} \right)\left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^3} + {x^2} - x - 1} \right) = {1^3} + {1^2} - 1 - 1 = 0\\\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0.2 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
e) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x - 1} \right) = 1 - 1 = 0\\\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}} = \frac{0}{2} = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\end{array}\)
cho lim \(\dfrac{f\left(x\right)-5}{x-1}=4\) khi x->1 , lim \(\dfrac{g\left(x\right)-1}{x-1}=5\) khi x->1
tinh lim \(\dfrac{\sqrt{f\left(x\right)\times g\left(x\right)+4}-1}{x-1}\)khi x->1
Bạn tham khảo:
Nếu \(lim\) (x->1) \(\dfrac{f\left(x\right)-5}{x-1}=2\) và lim (x->1) \(\dfrac{g\left(x\right)-1}{x-1}=3\) thì lim (x->1... - Hoc24
Không giống hoàn toàn, nhưng cách làm thì giống hoàn toàn
Cho hàm số y=f(x) xác định trên (a;b). Nếu \(\forall\left(x_o\right),x_n\ne x_o,l\text{imx}_n=x_o\Rightarrow l\text{imf}\left(x_n\right)=+\infty\) thì:
A. \(\lim\limits_{x->x_o}f\left(x\right)=L\)
B. \(\lim\limits_{x->x_o^-}f\left(x\right)=-\infty\)
C. \(\lim\limits_{x->x_o}f\left(x\right)=-\infty\)
D. \(\lim\limits_{x->x_o}f\left(x\right)=+\infty\)
\(\lim\limits_{x\rightarrow x_0}f\left(x\right)=+\infty\)
1) tính limx➞-∞( 4x5-3x2+1)
2) Tính lim(x➞4) \(\frac{1-x}{\left(x-4\right)^{^2}}\)
3)Cho hàm số f(x) = { (căn x) +1 nếu x≥0; 2x nếu x<0}
\(\lim\limits_{x\rightarrow-\infty}\left(4x^5-3x^2+1\right)=\lim\limits_{x\rightarrow-\infty}x^5\left(4-\frac{3}{x^3}+\frac{1}{x^5}\right)=-\infty.4=-\infty\)
\(\lim\limits_{x\rightarrow4}\frac{1-x}{\left(x-4\right)^2}=\frac{-3}{0}=-\infty\)
Câu tiếp theo đề thiếu, ko thấy yêu cầu gì hết
Quan sát đồ thị hàm số \(f\left( x \right) = x\) ở Hình 11.
a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\)
b) So sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) với \(f\left( 1 \right).\)
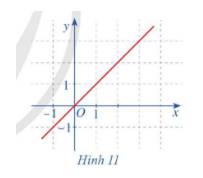
a) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} x = 1\)
b) \(f\left( 1 \right) = 1 \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right).\)
Chọn khẳng định đúng trong các khẳng định sau:
Câu 1:
A.Nếu lim|\(u_n\)|=+oo, thì lim\(u_n\)= +oo B. Nếu lim|\(u_n\)|=+oo, thì lim\(u_n\)=-oo
C.Nếu lim\(u_n\)=0, thì lim|\(u_n\)|=0 D.C.Nếu lim\(u_n\)=-a, thì lim|\(u_n\)|=a
Câu 2:
(I). f(x)=\(\frac{\sqrt{x+1}}{x-1}\) liên tục với mọi x≠1
(II). f(x)=sinx liên tục trên R
(III). f(x)=\(\frac{\left|x\right|}{x}\)liên tục tại x=1
A. Chỉ (I) đúng B. Chỉ (I) va (II) C, Chỉ (I) và (III) D. Chỉ (II) va (III)
Câu 1: đáp án C đúng (đáp án A và B hiển nhiên sai, đáp án D chỉ đúng khi a không âm)
Câu 2: (I) sai, vì với \(x< -1\) hàm ko xác định nên ko liên tục
(II) đúng do tính chất hàm sin
(III) đúng do \(\lim\limits_{x\rightarrow1}\frac{\left|x\right|}{x}=\frac{\left|1\right|}{1}=f\left(1\right)\)
Vậy đáp án D đúng
e) lim\(\dfrac{17}{x^2+1}\)(x-->+\(\infty\))
f) lim\(\dfrac{-2x^2+x-1}{3+x}\)(x-->+\(\infty\))
\(\lim\limits_{x\rightarrow+\infty}\dfrac{17}{x^2+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{17}{x^2}}{1+\dfrac{1}{x^2}}=\dfrac{0}{1}=0\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{-2x^2+x-1}{3+x}=\lim\limits_{x\rightarrow+\infty}x\left(\dfrac{-2+\dfrac{1}{x}-\dfrac{1}{x^2}}{\dfrac{3}{x}+1}\right)\)
Do \(\lim\limits_{x\rightarrow+\infty}x=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{-2+\dfrac{1}{x}-\dfrac{1}{x^2}}{\dfrac{3}{x}+1}\right)=-2< 0\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x\left(\dfrac{-2+\dfrac{1}{x}-\dfrac{1}{x^2}}{\dfrac{3}{x}+1}\right)=-\infty\)