Tính I = ∫ 0 1 1 4 - x 2 d x
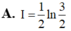
![]()
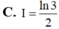
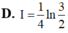
Giải phương trình:
1. (x - 4)2 - 25 = 0
2. (x - 3)2 - (x - 1)2 = 0
3. (x2 - 4)(2x +3) = (x2 - 4)(x - 1)
4. (x2 - 1) - (x + 1)(2 - 3x) = 0
5. x3 + x2 + x + 1 = 0
6. x3 + x2 - x - 1 = 0
7. 2x3 + 3x2 + 6x + 5 = 0
8. x4 - 4x3 - 19x2 + 106x - 120 = 0
9. (x2 - 3x + 2)(x2 + 15x + 56) + 8 = 0
1 ) \(\left(x-4\right)^2-25=0\)
\(\Leftrightarrow\left(x-4-5\right)\left(x-4+5\right)=0\)
\(\Leftrightarrow\left(x-9\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-1\end{matrix}\right.\)
2 ) \(\left(x-3\right)^2-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-3+x-1\right)\left(x-3-x+1\right)=0\)
\(\Leftrightarrow-2\left(2x-4\right)=0\)
\(\Leftrightarrow x=2.\)
3 ) \(\left(x^2-4\right)\left(2x+3\right)=\left(x^2-4\right)\left(x-1\right)\)
\(\Leftrightarrow\left(x^2-4\right)\left(2x+3-x+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=-4\end{matrix}\right.\)
4 ) \(\left(x^2-1\right)-\left(x+1\right)\left(2-3x\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-1-2+3x\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(4x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{4}\end{matrix}\right.\)
5 ) \(x^3+x^2+x+1=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-1\left(loại\right)\\x=-1.\end{matrix}\right.\)
6 ) \(x^3+x^2-x-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
7 ) \(2x^3+3x^2+6x+5=0\)
\(\Leftrightarrow2x^3+2x^2+x^2+x+5x+5=0\)
\(\Leftrightarrow2x^2\left(x+1\right)+x\left(x+1\right)+5\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x^2+x+5\right)\left(x+1\right)=0\)
\(\Leftrightarrow x=-1.\)
8 ) \(x^4-4x^3-19x^2+106x-120=0\)
\(\Leftrightarrow x^4-4x^3-19x^2+76x+30x-120=0\)
\(\Leftrightarrow x^3\left(x-4\right)-19x\left(x-4\right)+30\left(x-4\right)=0\)
\(\Leftrightarrow\left(x^3-19x+30\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left(x^3-8-19x+38\right)\left(x-4\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+4x+23\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
9 ) \(\left(x^2-3x+2\right)\left(x^2+15x+56\right)+8=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)\left(x+7\right)\left(x+8\right)+8=0\)
\(\Leftrightarrow\left(x^2+7x-x-7\right)\left(x^2+8x-2x-16\right)+8=0\)
\(\Leftrightarrow\left(x^2+6x-7\right)\left(x^2+6x-16\right)+8=0\)
Đặt \(x^2+6x-7=t\)
\(\Leftrightarrow t\left(t-9\right)+8=0\)
\(\Leftrightarrow t^2-9t+8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=8\\t=1\end{matrix}\right.\)
Khi t = 8 \(\Leftrightarrow x^2+6x-7=8\Leftrightarrow x^2+6x-15\Leftrightarrow\left[{}\begin{matrix}x=-3+2\sqrt{6}\\x=-3-2\sqrt{6}\end{matrix}\right.\)
Khi t = 1 \(\Leftrightarrow x^2+6x-7=1\Leftrightarrow x^2+6x-8=0\Leftrightarrow\left[{}\begin{matrix}x=-3+\sqrt{17}\\x=-3-\sqrt{17}\end{matrix}\right.\)
Vậy ........
Bài 1 : Tìm x thuộc Z , biết :
1. ( x - 1 ) ( x + 2 ) < 0
2. ( x + 1 ) ( 2x - 4 ) lớn hơn hoặc bằng 0
3.( \(x^2\) + 1 ) ( \(x^2\) - 4 ) nhỏ hơn hoặc bằng 0
4. | x| . ( \(x^2\) - 1 ) lớn hơn hoặc bằng 0 . \(\)
1) \(\left(x-1\right)\left(x+2\right)< 0\Leftrightarrow-2< x< 1\)
vậy \(x=-1;0\)
2) \(\left(x+1\right)\left(2x-4\right)\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le-1\end{matrix}\right.\)
vậy \(x=Z\backslash\left\{1;0\right\}\)
3) \(\left(x^2+1\right)\left(x^2-4\right)\le0\)
vì \(x^2+1\ne0\)
\(\Leftrightarrow x^2-4\le0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\le0\Leftrightarrow-2\le x\le2\)
vậy \(x=-2;-1;0;1;2\)
4) \(\left|x\right|\left(x^2-1\right)\ge0\)
ta có \(\left|x\right|\ge0\)
\(\Leftrightarrow x^2-1\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\x\le-1\end{matrix}\right.\)
vậy \(x=Z\backslash\left\{0\right\}\)
1: (x-1)(x+2)<0
=>-2<x<1
mà x là số nguyên
nên \(x\in\left\{-1;0\right\}\)
2: \(\left(x+1\right)\cdot\left(2x-4\right)>=0\)
=>x>=2 hoặc x<=-1
mà x là số nguyên
nên x=Z\{1;0}
3: \(\Leftrightarrow x^2-4< =0\)
=>-2<=x<=2
mà x là số nguyên
nên \(x\in\left\{-2;-1;0;1;2\right\}\)
4: =>(x2-1)>=0
=>x>=1 hoặc x<=-1
=>x=Z\{0}
a) (x+1/x-2)^2 + x+1/x-4 -3(2x-4/x-4)^2 = 0
b) 15x/x^2 +3x-4 - 1 = 12(1/x+4 + 1/3x-3)
c) x^2-4x+1/x+1 + 2 = - x^2-5x+1/2x+1
cho I = Limx→0 2(√3x+1 -1)/x và J = limx→-1 x2-x-2 / x+ 1. tính I-J
X
\(\lim\limits_{x\rightarrow0}\dfrac{2\left(\sqrt{3x+1}-1\right)}{x}=\lim\limits_{x\rightarrow0}\dfrac{6x}{x\left(\sqrt{3x+1}+1\right)}=\lim\limits_{x\rightarrow0}\dfrac{6}{\sqrt{3x+1}+1}=3\)
\(\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(x-2\right)}{x+1}=\lim\limits_{x\rightarrow-1}\left(x-2\right)=-3\)
\(\Rightarrow I-J=6\)
Tìm x ; y biết
I 2x-4 I + I x+3 I = 5
a(x-1)(x-5)=1 (với a khác 0 )
(x + y -1/4)2 + (x-y+1/5)2=0
{xI+2yI=5xI+yI−3=0
{xI+2yI=5xI+yI−3=0
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Bài 1: Cho x+y+z =0 và x^2+ y^2 + z^2=14
Tính S= x^4+y^4+z^4
Bài 2: Cho 1/x +1/y +1/z= 13 và x+y+z= xyz
Tính S= 1/x^2 +1/y^2 +1/z^2
Bài 3: Cho a,b,c khác 0 và a+b+c = 0
Tính S= 1/ a^2+b^2-c^2 + 1/b^2+c^2-a^2 +1/ c^2+a^2-b^2
Bài 4: Cho x>y>0 và 3x^2+ 3y^2 = 10xy
Tính S= x-y / x+y
Bài 5: Cho a^2+4b+4 và b^2+ 4c+4 và c^2+ 4a+4 = 0
Tính S= a^18+ b^18+ c^18
Bài 1: cho x+y+z=0 và x^2+y^2+z^2=14 .Tính S=x^4+y^4+z^4
Bài 2: cho x>y>0 và a+b+c=0.Tính S= \(\dfrac{1}{a^2+b^2-c^2}\)+\(\dfrac{1}{b^2+c^2-a^2}\)+\(\dfrac{1}{c^2+a^2-b^2}\)
bài 3: cho a^2 +4b +4=0
b^2 +4c+4=0
c^2 +4a+4=0 .Tính S=a^18+b^18+c^18
1,
\(x^2+y^2+y^2=14\)
\(\Rightarrow\left(x+y+z\right)^2-2xy-2yz-2zx=14\)
\(\Rightarrow-2\left(xy+yz+zx\right)=14\)
\(\Rightarrow xy+yz+zx=-7\)
\(\Rightarrow\left(xy+yz+zx\right)^2=49\)
\(\Leftrightarrow x^2y^2+y^2z^2+z^2x^2+2x^2yz+2xy^2z+2xyz^2=49\)
\(\Leftrightarrow x^2y^2+y^2z^2+z^2x^2+2xyz\left(x+y+z\right)=49\)
\(\Leftrightarrow x^2y^2+y^2z^2+z^2x^2=49\)
Ta có: \(x^4+y^4+z^4\)
\(=\left(x^2+y^2+z^2\right)^2-2x^2y^2-2y^2z^2-2z^2x^2\)
\(=14^2-2\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(=14^2-2.49\)
\(=196-98\)
\(=98\)
Tìm x, biết:
1) 1/3. x + 2/5. (x - 1) = 0
2) (2 x - 3).(6 - 2 x) =0
3) (3 x -1).(-1/2 x + 5) = 0
4) (2 x + 3/5)2 - 9/25 = 0
Tính:
1) 4/2.4 + 4/4.6 + 4/6.8 + ... + 4/2008.2010
2) 1/18 + 1/54 + 1/108 + ... +1/990
\(a,\frac{1}{3}x+\frac{2}{5}x-\frac{2}{5}=0\)
\(\frac{11}{15}x=\frac{2}{5}\)
\(x=\frac{6}{11}\)
b,\(\left(2x-3\right).\left(6-2x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x-3=0\\6-2x=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{3}{2}\\x=3\end{cases}}\)
Vậy
\(\left(3x-1\right).\left(-\frac{1}{2}x+5\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x-1=0\\-\frac{1}{2}x+5=0\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=10\end{cases}}}\)\
Vậy
Bài 1:
Cho \(x+y+z=0 \)
CMR: \(x^3+y^3+z^3=3xy\)
Bài 2:
Cho \(a+b+c=0\) và \(a^2+b^2+x^2=1\)
Tính \(a^4+b^4+c^4\)
Bài 1
\(x+y+z=0\)
\(\Leftrightarrow x+y=-z\)
\(\Leftrightarrow\left(x+y\right)^3=-z^3\)
\(\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=-z^3\)
\(\Leftrightarrow x^3+y^3-3xyz=-z^3\) (vì x+y=-z)
\(\Leftrightarrow x^3+y^3+z^3=3xyz\)