Mik cần trình bày rõ ràng ạ, mik cảm ơn
M9
Những câu hỏi liên quan
Mik cần trình bày rõ ràng ạ, mik cảm ơn
Đọc tiếp
Mik cần trình bày rõ ràng ạ, mik cảm ơn
PTĐTTNT : 2x-1-x^2
mong các bạn trình bày rõ ràng giúp mik ạ! mik cảm ơn.
\(2x-1-x^2\\ =x+x-1-x^2\\ =\left(x-x^2\right)+\left(x-1\right)\\ =-x\left(x-1\right)+\left(x-1\right)\\ =\left(x-1\right)\left(1-x\right)\)
Đúng 1
Bình luận (0)
2x - 1 - x²
= -x² + 2x - 1
= -(x² - 2x + 1)
= -(x - 1)²
Đúng 0
Bình luận (0)
Một hình bình hành có đáy dài 18 cm, chiều cao bằng 2/3 độ dài đáy. Diện tích hình đó là: Mn trình bày rõ ràng hộ mik với ạ cảm ơn
Chiều cao hình bình hành là:
`18xx 2/3=12`(cm)
Diện tích hình bình hành là:
`18 xx 12 = 216`(cm2)
Đáp số: 216cm2
Đúng 2
Bình luận (0)
chiều cao là
18 x 2/3= 12 (cm)
Diện tích là
18x12= 216 (cm2)
Đúng 2
Bình luận (0)
bài giải :
chiều cao hình bình hành là :
18 x 2/3 = 12 (cm)
diện tích hình bình hành là :
18 x 12 = 216 (cm2)
đáp số : ....
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
( x + 2,7 ) : 4,9 =25,3
các bn trình bày rõ ràng dễ hiểu hộ mik nha. mik cảm ơn
( x + 2,7 ) : 4,9 = 25,3
( x + 2,7 ) = 25,3 x 4,9
x + 2,7 = 123,97
x = 123,97 - 2,7
x = 121,27
Đúng 0
Bình luận (0)
(x+2,7):4,9=25,3
x+2,7 =25,3x4,9
x+2,7 =123,97
x =123,97-2,7
x =121,27
Đúng 0
Bình luận (0)
(x + 2,7) : 4,9 = 25,3
x + 27 = 25,3 x 4,9
x + 27 = 123,97
x = 123,97 - 27
x = 96,97
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi giúp mik voiwsii mai mik học rồi mà mik chx làm xong, cho mi câu trả lời chi tiết và rõ ràng nhất với ạ, xong thì mik sẽ tick mik cảm ơnnnnn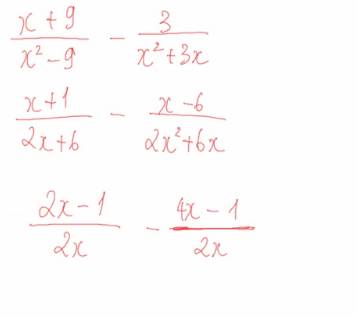
Đây là cách trình bày :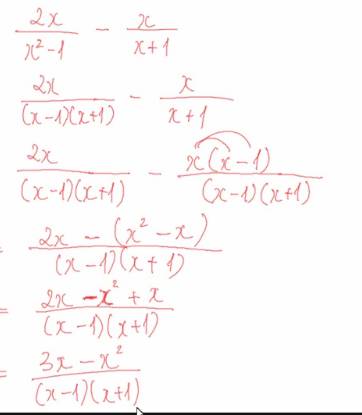
a) \(\dfrac{x+9}{x^2-9}\)-\(\dfrac{3}{x^2+3x}\) = \(\dfrac{x+9}{\left(x-3\right)\left(x+3\right)}\)-\(\dfrac{3}{x\left(x+3\right)}\)
= \(\dfrac{x^2+9x-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{x^2+6x+9}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{x+3}{x\left(x-3\right)}\)
Đúng 1
Bình luận (0)
GIẢI GIÚP EM CÂU 5 TRÌNH BÀY RÕ RÀNG DỄ HIẾU VỚI Ạ , EM CẢM ƠN 
Câu 5:
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật
Đúng 0
Bình luận (0)
người ơi giúp mik với mik đg cần gấp lắm ạ!! Còn 20p nữa là mik học rồi nhưng mik vẫn còn 3 câu chx tính xong, mọi người giúp mik với ạ, cho mik câu trả lời chi tiết và rõ ràng các bước nhất với ạ!, mi cảm ơn! Xong thì mik sẽ tick ạ( cái ảnh thứ nhất là cách làm ạ.)
Đọc tiếp
người ơi giúp mik với mik đg cần gấp lắm ạ!! Còn 20p nữa là mik học rồi nhưng mik vẫn còn 3 câu chx tính xong, mọi người giúp mik với ạ, cho mik câu trả lời chi tiết và rõ ràng các bước nhất với ạ!, mi cảm ơn! Xong thì mik sẽ tick ạ( cái ảnh thứ nhất là cách làm ạ.)


a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
Đúng 1
Bình luận (0)

giải, trình bày rõ ràng đầy đủ và vẽ hình giúp mình với ạ mình cảm ơn
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
Đúng 0
Bình luận (0)
Mọi người ơi giúp mik voiwsii mai mik học rồi mà mik chx làm xong, cho mi câu trả lời chi tiết và rõ ràng nhất với ạ, xong thì mik sẽ tick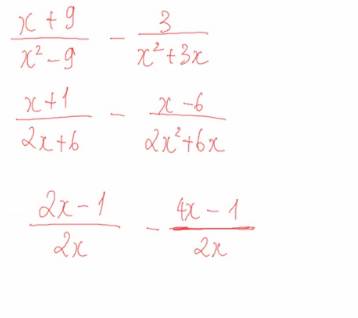
Đây là cách trình bày :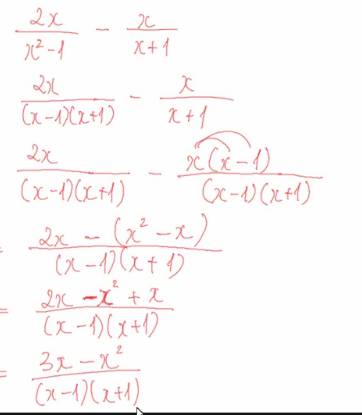
\(\dfrac{x+9}{x^2-9}-\dfrac{3}{x^2+3x}\)
= \(\dfrac{x+9}{\left(x-3\right).\left(x+3\right)}-\dfrac{3}{x.\left(x+3\right)}\)
=\(\dfrac{\left(x+9\right).x}{\left(x-3\right).\left(x+3\right).x}-\dfrac{3.\left(x-3\right)}{x.\left(x+3\right).\left(x-3\right)}\)
=\(\dfrac{x^2+9x}{x\left(x-3\right)\left(x+3\right)}-\dfrac{3x-9}{x\left(x-3\right)\left(x+3\right)}\)
=\(\dfrac{x^2+9-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
=\(\dfrac{x^2-3x+18}{3\left(x-3\right)\left(x+3\right)}\)
Đúng 2
Bình luận (0)








