Cho hình vẽ, biết E F P ^ = 47 o . Hai đường thẳng MN và PQ song song với nhau khi:
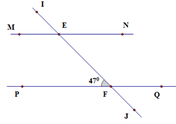
A. M E F ^ = 133 °
B. M E I ^ = 47 °
C. I E N ^ = 133 °
D. Cả A,B,C đều đúng
cho hình thang MNPQ (MN//PQ,MN<PQ) a là giao của MP và NQ
a) cho AM/AQ =3/5 và AN =6cm , MN =7cm
Tính AP =?, QP=?
b,MP giao NQ tại O , kẻ đường thẳng qua O và song song với MN, PQ , dường thẳng này cắt MQ tại E cắt PN tại F . cm OE=OF
b: Xét hình thang MNPQ có EF//QP
nên ME/MQ=NF/NP(1)
Xét ΔMQP có EO//QP
nên EO/QP=ME/MQ(2)
Xét ΔNQP có OF//QP
nên OF/QP=NF/NP(3)
Từ (1), (2) và (3) suy ra OE/QP=OF/QP
hay OE=OF
cho hình thang MNPQ ( MN là đáy nhỏ) hai đường chéo MP và NQ cắt nhau tại O. Biết NMP=MNQ , qua O vẽ đường thẳng EF // PQ (E thuộc MQ, F thuộc NP) chứng minh NMQP, FEQP , MNFE là hình thang cân
ta có MNPQ là hình thang=>MN//PQ
mà \(=\angle\left(NMP\right)=\angle\left(MNQ\right)=>\angle\left(NQP\right)=\angle\left(MPQ\right)\)
=>tam giác MNO cân tại O=>MO=NO
=>tam giác QOP cân tại O=>OQ=Op
=>MO+OP=NO+OQ=>NQ=MP
=>MNPQ là hình thang cân
\(=>\angle\left(M\right)=\angle\left(N\right)\left(1\right)\)
\(\angle\left(Q\right)=\angle\left(P\right)\left(2\right)\)
mà EF//PQ=>EF//MN
=>MNFE là hình thang(3)
từ (1)(3)=>MNFE là hình thang cân
=>EFPQ là hình thang(4)
(2)(4)=>EFPQ là hình thang cân
Ta có: \(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{ONM}=\widehat{OQP}\)
mà \(\widehat{OMN}=\widehat{ONM}\)
nên \(\widehat{OPQ}=\widehat{OQP}\)
Xét ΔOMN có \(\widehat{OMN}=\widehat{ONM}\)
nên ΔOMN cân tại O
Xét ΔOPQ có \(\widehat{OPQ}=\widehat{OQP}\)
nên ΔOPQ cân tại O
Ta có: OM+OP=MP
ON+OQ=QN
mà OM=ON
và OP=OQ
nên MP=QN
Hình thang MNPQ có MP=QN
nên MNPQ là hình thang cân
Suy ra: \(\widehat{EMN}=\widehat{FNM}\) và \(\widehat{EQP}=\widehat{FPQ}\)
Hình thang EMNF có \(\widehat{EMN}=\widehat{FNM}\)
nên EMNF là hình thang cân
Hình thang EQPF có \(\widehat{EQP}=\widehat{FPQ}\)
nên EQPF là hình thang cân
Vẽ đường thẳng MN đi qua điểm O và song song với đường thẳng PQ

Vẽ đường thẳng MN đi qua điểm O song song đường thẳng PQ
Cho hình vẽ sau biết đường thẳng m cắt hai đường thẳng song song a và b . Biết A³ = 47° tính số đo ^B¹
Hình đâu em nhỉ, không có hình thì cô chịu nhé
1.Cho tứ giác ABCD có hai đường chéo chắt nhau tại O. Đường thẳng vẽ từ A song song với BC cắt BD tại M. Đường thẳng vẽ từ B song song với AD cắt AC tại N. Chứng minh:
a) OD/OB=OA/ON
b) OB*OA= OM*OC
2.Cho hình bình hành ABCD. Từ điểm E trên cạnh AB vẽ EG song song AC (G thuộc BC) vẽ GH song song BD (H thuộc CD) vẽ HF song song AC ( F thuộc AD). Chứng minh:
a)AE/EB= CG/GB
b)CG*HD = GB*CH
c) CH/HD=AF/FD
3. Cho hình thang ABCD (AB song song CD) một đường thẳng song song với AB cắt các đoạn thẳng AD,AC,BD,BC theo thứ tự tại M,N,P,Q. Chứng minh:
a)MN*AD=DC*AM
b)MN=PQ
Giúp em giải với chiều nay em nộp rồi ạ!
Cho AB và CD là hai đoạn thẳng song song và bằng nhau. MN và PQ là các hình
chiếu của chúng trên cùng một đường thẳng khác. Chứng minh MN= PQ.
Hình bình hành MNPQ ( MN song song PQ). I là giao điểm của MP và NQ . Qua I kẻ đường thẳng song song với MN cắt MQ ở E và cắt NP ở F . Chứng minh I là trung điểm của EF
Theo tính chất: Hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường, ta suy ra I là trung điểm của NQ và MP.
Xét tam giác MQN có I là trung điểm NQ, IE // MN nên IE là đường trung bình tam giác.
Vậy nên IE = MN/2
Tương tự IF là đường trung bình tam giác ANP nên IF = MN/2
Vậy nên IE = IF hay I là trung điểm EF.
Cho hai điểm P , Q và một đường thẳng a không chứa P , Q ( hãy vẽ hình ) Nêu cách tìm một điểm M trên đường thẳng a sao cho ba điểm M , P , Q thẳng hàng . Hãy xét các trường hợp sau và cho biết trong trường hợp nào thì tìm được điểm M như thế :
- Đường thẳng PQ cắt đường thẳng a
- Đường thẳng PQ không cắt đường thẳng a ( PQ song song với a )
VẼ HÌNH NHA ! Ai nhanh được ****
cho hình thang MNPQ ( MN là đáy nhỏ) hai đường chéo MP và NQ cắt nhau tại O. Biết NMP=MNQ , qua O vẽ đường thẳng EF // PQ( E thuộc MQ, F thuộc NQ) chứng minh NMQP , MNFE là hình thang